Difference between revisions of "Compactified Morse trajectory spaces"

From Polyfolds.org
Jump to: navigation, search
m
m
Line 18: Line 18:
 
</center>
 
</center>
  
−
'''TODO:''' smooth evaluation maps <math>{\rm ev}^\pm</math>, length <math>\ell: \overline \mathcal{M}(L,L) \to [0,\infty]</math> given by <math>\ell(\gamma)= a</math> and <math>\ell(\underline{\gamma})=\infty</math> for all generalized (''broken'') Morse trajectories <math>\underline{\gamma}</math>
+
'''TODO:''' smooth evaluation maps <math>{\rm ev}^\pm</math>,  
 +
 
 +
length <math>\ell: \overline \mathcal{M}(L,L) \to [0,\infty]</math> given by <math>\ell(\gamma)= a</math> for <math>\gamma: [0,a] \to L</math> and <math>\ell(\underline{\gamma})=\infty</math> for all generalized (''broken'') Morse trajectories <math>\underline{\gamma}</math>

Revision as of 10:53, 24 May 2017

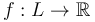Consider a smooth manifold L equipped with a Morse function f:L\to \mathbb{R} and a metric so that the gradient vector field \nabla f satisfies the Morse-Smale conditions. Then the Morse trajectory spaces

{\begin{alignedat}{4}{\mathcal {M}}(L,L)&=\{\gamma :&[0,a]\;\;\to L&\,|\,{\dot \gamma }=-\nabla f(\gamma ),a\geq 0\},\\{\mathcal {M}}(p^{-},L)&=\{\gamma :&(-\infty ,0]\to L&\,|\,{\dot \gamma }=-\nabla f(\gamma ),\lim _{{s\to -\infty }}\gamma (s)=p^{-}\},\\{\mathcal {M}}(L,p^{+})&=\{\gamma :&[0,\infty )\;\to L&\,|\,{\dot \gamma }=-\nabla f(\gamma ),\lim _{{s\to +\infty }}\gamma (s)=p^{+}\},\\{\mathcal {M}}(p^{-},p^{+})&=\{\gamma :&\mathbb{R} \;\;\;\to L&\,|\,{\dot \gamma }=-\nabla f(\gamma ),\lim _{{s\to \pm \infty }}\gamma (s)=p^{\pm }\}/\mathbb{R} .\end{alignedat}}

can - under an additional technical assumption specified in [1] - be compactified to smooth manifolds with boundary and corners {\mathcal {M}}(\cdot ,\cdot ). These compactifications are constructed such that the codimension-1 strata of the boundary are given by single breaking at a critical point (except in the first case we have to add one copy of L to represent trajectories of length 0),

\textstyle \partial ^{1}\overline {\mathcal {M}}(\cdot ,\cdot )\;=\;{\bigl (}\;L\cup \;{\bigr )}\;\bigsqcup _{{q\in {\text{Crit}}(f)}}\overline {\mathcal {M}}(\cdot ,q)\times \overline {\mathcal {M}}(q,\cdot ).

TODO: smooth evaluation maps {{\rm {ev}}}^{\pm },

length \ell :\overline {\mathcal {M}}(L,L)\to [0,\infty ] given by \ell (\gamma )=a for \gamma :[0,a]\to L and \ell (\underline {\gamma })=\infty for all generalized (broken) Morse trajectories \underline {\gamma }

Retrieved from "http://www.polyfolds.org/index.php?title=Compactified_Morse_trajectory_spaces&oldid=288"