Difference between revisions of "Problems on Deligne-Mumford spaces"
From Polyfolds.org
Natebottman (Talk | contribs) |
Natebottman (Talk | contribs) |
||
| Line 6: | Line 6: | ||
As shown in [Auroux, Ex. 2.6], <math>\overline\mathcal{M}_4</math> is homeomorphic to a closed interval, with one endpoint corresponding to a collision of the first two inputs <math>z_1, z_2</math> and the other corresponding to a collision of <math>z_2, z_3</math>. | As shown in [Auroux, Ex. 2.6], <math>\overline\mathcal{M}_4</math> is homeomorphic to a closed interval, with one endpoint corresponding to a collision of the first two inputs <math>z_1, z_2</math> and the other corresponding to a collision of <math>z_2, z_3</math>. | ||
Work out which polygon/polyhedron <math>\overline\mathcal{M}_5, \overline\mathcal{M}_6</math> are equal to. | Work out which polygon/polyhedron <math>\overline\mathcal{M}_5, \overline\mathcal{M}_6</math> are equal to. | ||
| + | (Keep in mind that when <math>\geq 3</math> marked points collide simultaneously, there is a continuous family | ||
Revision as of 14:54, 26 May 2017
poset underlying associahedra
As described in Deligne-Mumford space, for any 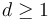 ,
, 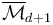 is a
is a  -dimensional manifold with boundary and corners which parametrizes nodal trees of disks with
-dimensional manifold with boundary and corners which parametrizes nodal trees of disks with 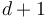 marked points, one of them distinguished (we think of the
marked points, one of them distinguished (we think of the 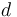 undistinguished resp. 1 distinguished marked points as "input" resp. "output" marked points).
As shown in [Auroux, Ex. 2.6],
undistinguished resp. 1 distinguished marked points as "input" resp. "output" marked points).
As shown in [Auroux, Ex. 2.6], 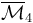 is homeomorphic to a closed interval, with one endpoint corresponding to a collision of the first two inputs
is homeomorphic to a closed interval, with one endpoint corresponding to a collision of the first two inputs 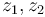 and the other corresponding to a collision of
and the other corresponding to a collision of 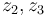 .
Work out which polygon/polyhedron
.
Work out which polygon/polyhedron  are equal to.
(Keep in mind that when
are equal to.
(Keep in mind that when  marked points collide simultaneously, there is a continuous family
marked points collide simultaneously, there is a continuous family