Difference between revisions of "Problems on Deligne-Mumford spaces"
Natebottman (Talk | contribs) (→poset underlying associahedra) |
Natebottman (Talk | contribs) |
||
| Line 7: | Line 7: | ||
Work out which polygon/polyhedron <math>\overline\mathcal{M}_5, \overline\mathcal{M}_6</math> are equal to. | Work out which polygon/polyhedron <math>\overline\mathcal{M}_5, \overline\mathcal{M}_6</math> are equal to. | ||
(Keep in mind that when <math>\geq 3</math> marked points collide simultaneously, there is a continuous family of ways that this collision can take place.) | (Keep in mind that when <math>\geq 3</math> marked points collide simultaneously, there is a continuous family of ways that this collision can take place.) | ||
| + | |||
| + | == 2-, 3-dimensional examples of "the original" Deligne-Mumford space == | ||
| + | |||
| + | Define <math>\mathcal{M}_{0,d+1}(\mathbb{C})</math> to be the moduli space | ||
| + | <center><math> | ||
| + | \mathcal{M}_{0,d+1}(\mathbb{C}) := \bigl\{ \underline{z} = \{z_0,\ldots,z_d\}\in \mathbb{CP}^1 \;\text{pairwise disjoint} \bigr\}/_\sim, | ||
| + | </math></center> | ||
| + | where two configurations are identified if one can be taken to the other by a Moebius transformation. | ||
| + | We can compactify to form <math>\overline\mathcal{M}_{0,d+1}(\mathbb{C})</math> by including trees of spheres, any neighboring pair of which is attached to one another at a pair of points. | ||
| + | (A detailed construction of <math>\overline\mathcal{M}_{0,d+1}(\mathbb{C})</math> can be found in [big McDuff-Salamon, App. D].) | ||
| + | Make the identifications (don't worry too much about rigor) <math>\overline\mathcal{M}_{0,3}(\mathbb{C}) \cong \mathrm{pt}</math>, <math>\overline\mathcal{M}_{0,4}(\mathbb{C}) \cong \mathbb{CP}^1</math>, and <math>\overline\mathcal{M}_{0,5}(\mathbb{C}) \cong (\mathbb{CP}^1\times\mathbb{CP}^1) \# 3\overline{\mathbb{CP}}^2</math>. | ||
== poset underlying associahedra == | == poset underlying associahedra == | ||
Revision as of 06:13, 27 May 2017
2-, 3-dimensional associahedra
As described in Deligne-Mumford space, for any 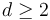 , the associahedron
, the associahedron 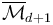 is a
is a  -dimensional manifold with boundary and corners which parametrizes nodal trees of disks with
-dimensional manifold with boundary and corners which parametrizes nodal trees of disks with 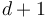 marked points, one of them distinguished (we think of the
marked points, one of them distinguished (we think of the 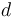 undistinguished resp. 1 distinguished marked points as "input" resp. "output" marked points).
As shown in [Auroux, Ex. 2.6],
undistinguished resp. 1 distinguished marked points as "input" resp. "output" marked points).
As shown in [Auroux, Ex. 2.6], 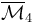 is homeomorphic to a closed interval, with one endpoint corresponding to a collision of the first two inputs
is homeomorphic to a closed interval, with one endpoint corresponding to a collision of the first two inputs 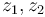 and the other corresponding to a collision of
and the other corresponding to a collision of 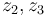 .
Work out which polygon/polyhedron
.
Work out which polygon/polyhedron  are equal to.
(Keep in mind that when
are equal to.
(Keep in mind that when  marked points collide simultaneously, there is a continuous family of ways that this collision can take place.)
marked points collide simultaneously, there is a continuous family of ways that this collision can take place.)
2-, 3-dimensional examples of "the original" Deligne-Mumford space
Define  to be the moduli space
to be the moduli space

where two configurations are identified if one can be taken to the other by a Moebius transformation.
We can compactify to form 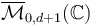 by including trees of spheres, any neighboring pair of which is attached to one another at a pair of points.
(A detailed construction of
by including trees of spheres, any neighboring pair of which is attached to one another at a pair of points.
(A detailed construction of 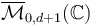 can be found in [big McDuff-Salamon, App. D].)
Make the identifications (don't worry too much about rigor)
can be found in [big McDuff-Salamon, App. D].)
Make the identifications (don't worry too much about rigor)  ,
,  , and
, and  .
.
poset underlying associahedra
The associahedron 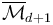 can be given the structure of a stratified space, where the underlying poset is called
can be given the structure of a stratified space, where the underlying poset is called 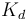 and consists of stable rooted ribbon trees with
and consists of stable rooted ribbon trees with 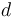 leaves.
Similarly to the setup in Moduli spaces of pseudoholomorphic polygons, a stable rooted ribbon tree is a tree
leaves.
Similarly to the setup in Moduli spaces of pseudoholomorphic polygons, a stable rooted ribbon tree is a tree 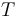 satisfying these properties:
satisfying these properties:
-
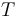 has
has 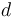 leaves and 1 root (in our terminology, the root has valence 1 but is not counted as a leaf);
leaves and 1 root (in our terminology, the root has valence 1 but is not counted as a leaf); -
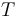 is stable, i.e. every main vertex (=neither a leaf nor the root) has valence at least 3;
is stable, i.e. every main vertex (=neither a leaf nor the root) has valence at least 3; -
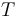 is a ribbon tree, i.e. the edges incident to any vertex are equipped with a cyclic ordering.
is a ribbon tree, i.e. the edges incident to any vertex are equipped with a cyclic ordering.
To define the partial order, we declare 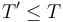 if we can contract some of the interior edges in
if we can contract some of the interior edges in 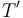 to get
to get 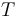 ; we declare that
; we declare that 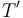 is in the closure of
is in the closure of 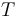 if
if 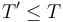 .
Write the closure of the stratum corresponding to
.
Write the closure of the stratum corresponding to 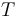 as a product of lower-dimensional
as a product of lower-dimensional 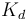 's.
Which tree corresponds to the top stratum of
's.
Which tree corresponds to the top stratum of 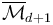 ?
To the codimension-1 strata of
?
To the codimension-1 strata of 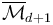 ?
?
...and, to the operadically initiated (or willing to dig around a little at [[1]]): show that the collection 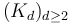 can be given the structure of an operad (which is to say that for every
can be given the structure of an operad (which is to say that for every 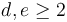 and
and 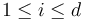 there is a composition operation
there is a composition operation 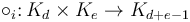 which splices
which splices 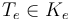 onto
onto 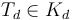 by identifying the outgoing edge of
by identifying the outgoing edge of 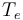 with the
with the 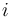 -th incoming edge of
-th incoming edge of 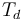 , and that these operations satisfy some coherence conditions).
Next, show that algebras / categories over the operad
, and that these operations satisfy some coherence conditions).
Next, show that algebras / categories over the operad 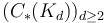 of cellular chains on
of cellular chains on 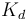 are the same thing as
are the same thing as 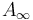 algebra / categories.
algebra / categories.