Difference between revisions of "Moduli spaces of pseudoholomorphic polygons"

From Polyfolds.org
Jump to: navigation, search
(Created page with "To construct the moduli spaces from which the composition maps are defined we fix an auxiliary almost complex structure <math>J:TM\to TM</math> which is compatible with the sy...")
 
Line 1: Line 1:
 
To construct the moduli spaces from which the composition maps are defined we fix an auxiliary almost complex structure <math>J:TM\to TM</math> which is compatible with the symplectic structure in the sense that <math>\omega(\cdot, J \cdot)</math> defines a metric on <math>M</math>. (Unless otherwise specified, we will use this metric in all following constructions.)
 
To construct the moduli spaces from which the composition maps are defined we fix an auxiliary almost complex structure <math>J:TM\to TM</math> which is compatible with the symplectic structure in the sense that <math>\omega(\cdot, J \cdot)</math> defines a metric on <math>M</math>. (Unless otherwise specified, we will use this metric in all following constructions.)
 
Then given Lagrangians <math>L_0,\ldots,L_d\subset M</math> and generators <math>x_0\in\text{Crit}(L_0,L_d), x_1\in\text{Crit}(L_0,L_1), \ldots, x_d\in\text{Crit}(L_{d-1},L_d)</math> of their morphism spaces, we need to specify the moduli space <math>\overline\mathcal{M}(x_0;x_1,\ldots,x_d)</math>.  
 
Then given Lagrangians <math>L_0,\ldots,L_d\subset M</math> and generators <math>x_0\in\text{Crit}(L_0,L_d), x_1\in\text{Crit}(L_0,L_1), \ldots, x_d\in\text{Crit}(L_{d-1},L_d)</math> of their morphism spaces, we need to specify the moduli space <math>\overline\mathcal{M}(x_0;x_1,\ldots,x_d)</math>.  
−
We will do this below by combining the following two special cases.
+
We will do this below by combining two special cases.
  
 
== Disk trees for a fixed Lagrangian ==
 
== Disk trees for a fixed Lagrangian ==

Revision as of 20:22, 20 May 2017

To construct the moduli spaces from which the composition maps are defined we fix an auxiliary almost complex structure J:TM\to TM which is compatible with the symplectic structure in the sense that \omega (\cdot ,J\cdot ) defines a metric on M. (Unless otherwise specified, we will use this metric in all following constructions.) Then given Lagrangians L_{0},\ldots ,L_{d}\subset M and generators x_{0}\in {\text{Crit}}(L_{0},L_{d}),x_{1}\in {\text{Crit}}(L_{0},L_{1}),\ldots ,x_{d}\in {\text{Crit}}(L_{{d-1}},L_{d}) of their morphism spaces, we need to specify the moduli space \overline {\mathcal {M}}(x_{0};x_{1},\ldots ,x_{d}). We will do this below by combining two special cases.

Disk trees for a fixed Lagrangian

If the Lagrangians are all the same, L_{0}=L_{1}=\ldots =L_{d}=:L, then our construction is based on pseudoholomorphic disks

u:D\to M,\qquad u(\partial D)\subset L,\qquad \overline \partial _{J}u=0.



Pseudoholomorphic polygons for pairwise transverse Lagrangians

If each consecutive pair of Lagrangians is transverse, i.e. L_{0}\pitchfork L_{1},L_{1}\pitchfork L_{2},\ldots ,L_{{d-1}}\pitchfork L_{d},L_{d}\pitchfork L_{0}, then our construction is based on pseudoholomorphic polygons

u:\Sigma \to M,\qquad u((\partial \Sigma )_{i})\subset L_{i},\qquad \overline \partial _{J}u=0,

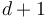where \Sigma =D\setminus \{z_{0},\ldots ,z_{d}\} is a disk with d+1 boundary punctures in counter-clockwise order z_{0},\ldots ,z_{d}\subset \partial D, and (\partial \Sigma )_{i} denotes the boundary component between z_{i},z_{{i+1}} (resp. between z_{{d}},z_{0} for i=d).



General moduli space of pseudoholomorphic polygons

Make up for differences in Hamiltonian symplectomorphisms applied to each Lagrangian by a domain-dependent Hamiltonian perturbation to the Cauchy-Riemann equation




Finally, the symplectic area function \omega :\overline {\mathcal {M}}(x_{0};x_{1},\ldots ,x_{d})\to \mathbb{R} in each case is given by TODO

Retrieved from "http://www.polyfolds.org/index.php?title=Moduli_spaces_of_pseudoholomorphic_polygons&oldid=141"