Difference between revisions of "Moduli spaces of pseudoholomorphic polygons"
m (→General moduli space of pseudoholomorphic polygons) |
m |
||
| Line 31: | Line 31: | ||
# The pseudoholomorphic polygon <math>(\underline{z}, u )</math> is stable in the sense that the map <math>u:\Sigma_{\underline{z}}\to M</math> is nonconstant if the number of marked points is <math>d+1<3</math>. | # The pseudoholomorphic polygon <math>(\underline{z}, u )</math> is stable in the sense that the map <math>u:\Sigma_{\underline{z}}\to M</math> is nonconstant if the number of marked points is <math>d+1<3</math>. | ||
| − | Here two pseudoholomorphic polygons are equivalent <math>(\underline{z}, u) \sim (\underline{z}', u')</math> if there is a | + | Here two pseudoholomorphic polygons are equivalent <math>(\underline{z}, u) \sim (\underline{z}', u')</math> if there is a biholomorphism <math>\psi:D\to D</math> that preserves the marked points <math>\psi(z_i)= z'_i</math>, and relates the pseudoholomorphic polygons by reparametrization, <math>u = u'\circ\psi</math>. |
---- | ---- | ||
| Line 49: | Line 49: | ||
</div></div> | </div></div> | ||
| − | All isotropy groups of this uncompactified moduli space <math>\mathcal{M}(x_0;x_1,\ldots,x_d)</math> are trivial; that is any disk | + | All isotropy groups of this uncompactified moduli space <math>\mathcal{M}(x_0;x_1,\ldots,x_d)</math> are trivial; that is any disk biholomorphism <math>\psi:D\to D</math> that fixes <math>d+1\geq 1</math> marked points <math>\psi(z_i)= z_i</math>, and preserves a pseudoholomorphic map <math>u = u\circ\psi</math> must be the identity <math>\psi={\rm id}_D</math>. <div class="toccolours mw-collapsible mw-collapsed">'''Proof:'''<div class="mw-collapsible-content"> In case <math>d=2</math> this follows directly from the marked points, since any Mobius transformation that fixes three points is the identity. |
| − | In case <math>d=1</math> this requires both the stability and finite energy conditions: The group of | + | In case <math>d=1</math> this requires both the stability and finite energy conditions: The group of biholomorphisms that fix two marked points - i.e. the biholomorphisms of the strip - are shifts by <math>\R</math>. |
On the other hand, any J-holomorphic map <math>u:\R\times[0,1]\to M</math> has nonnegative energy density <math>u^*\omega= \bigl(|\partial_s u|^2+|\partial_t u|^2\bigr) ds\wedge dt</math> with <math>|\partial_s u|=|\partial_t u|</math>. | On the other hand, any J-holomorphic map <math>u:\R\times[0,1]\to M</math> has nonnegative energy density <math>u^*\omega= \bigl(|\partial_s u|^2+|\partial_t u|^2\bigr) ds\wedge dt</math> with <math>|\partial_s u|=|\partial_t u|</math>. | ||
If we now had nontrivial isotropy, i.e. <math>u(\tau+s,t)=u(s,t)</math> for some <math>\tau>0</math> and a nonconstant map <math>u</math>, then there would exist <math>s_0,t_0\in \R\times[0,1]</math> with <math>|\partial_s u(s_0,t_0)|=|\partial_t u(s_0,t_0)|>0</math> and thus | If we now had nontrivial isotropy, i.e. <math>u(\tau+s,t)=u(s,t)</math> for some <math>\tau>0</math> and a nonconstant map <math>u</math>, then there would exist <math>s_0,t_0\in \R\times[0,1]</math> with <math>|\partial_s u(s_0,t_0)|=|\partial_t u(s_0,t_0)|>0</math> and thus | ||
| Line 90: | Line 90: | ||
</math> | </math> | ||
</center> | </center> | ||
| − | Such disks (modulo reparametrization by | + | Such disks (modulo reparametrization by biholomorphisms of the disk) also arise from Gromov-compactifying other moduli spaces of pseudoholomorphic curves in which energy concentrates at a boundary point. |
To capture this bubbling algebraically, we work throughout with the Morse function <math>f:L\to\R</math> chosen in the setup of the morphism space <math>\text{Hom}(L,L)=\textstyle\sum_{x\in\text{Crit}(f)} \Lambda x</math>. We also choose a metric on <math>L</math> so that the gradient vector field <math>\nabla f</math> satisfies the Morse-Smale conditions and an additional technical assumption in [https://arxiv.org/abs/1205.0713] which guarantees a natural smooth manifold-with-boundary-and-corners structure on the [[compactified Morse trajectory spaces]] | To capture this bubbling algebraically, we work throughout with the Morse function <math>f:L\to\R</math> chosen in the setup of the morphism space <math>\text{Hom}(L,L)=\textstyle\sum_{x\in\text{Crit}(f)} \Lambda x</math>. We also choose a metric on <math>L</math> so that the gradient vector field <math>\nabla f</math> satisfies the Morse-Smale conditions and an additional technical assumption in [https://arxiv.org/abs/1205.0713] which guarantees a natural smooth manifold-with-boundary-and-corners structure on the [[compactified Morse trajectory spaces]] | ||
<math> \overline\mathcal{M}(L,L) , \overline\mathcal{M}(p^-,L), \overline\mathcal{M}(L,p^+), \overline\mathcal{M}(p^-,p^+) </math> for <math>p^\pm\in\text{Crit}(f)</math>. | <math> \overline\mathcal{M}(L,L) , \overline\mathcal{M}(p^-,L), \overline\mathcal{M}(L,p^+), \overline\mathcal{M}(p^-,p^+) </math> for <math>p^\pm\in\text{Crit}(f)</math>. | ||
| Line 150: | Line 150: | ||
Finally, two pseudoholomorphic disk trees are equivalent <math>(T, \underline{\gamma}, \underline{z}, \underline{u} ) \sim (T', \underline{\gamma}', \underline{z}', \underline{u}')</math> if | Finally, two pseudoholomorphic disk trees are equivalent <math>(T, \underline{\gamma}, \underline{z}, \underline{u} ) \sim (T', \underline{\gamma}', \underline{z}', \underline{u}')</math> if | ||
<div class="toccolours mw-collapsible mw-collapsed"> | <div class="toccolours mw-collapsible mw-collapsed"> | ||
| − | there is a tree isomorphism <math>\zeta:T\to T'</math> and a tuple of disk | + | there is a tree isomorphism <math>\zeta:T\to T'</math> and a tuple of disk biholomorphisms <math>(\psi_v:D\to D)_{v\in V^m}</math> |
| − | which preserving the tree | + | which preserving the tree, Morse trajectories, marked points, and pseudoholomorphic curves in the sense that |
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
* <math>\zeta</math> preserves the tree structure and order of edges; | * <math>\zeta</math> preserves the tree structure and order of edges; | ||
| − | |||
*<math>\underline{\gamma}_e=\underline{\gamma}'_{\zeta(e)}</math> for every <math>e\in E</math>; | *<math>\underline{\gamma}_e=\underline{\gamma}'_{\zeta(e)}</math> for every <math>e\in E</math>; | ||
* <math>\psi_v(z^v_e)= {z'}^{\zeta(v)}_{\zeta(e)}</math> for every <math>v\in V^m</math> and adjacent edge <math>e\in E_v</math>; | * <math>\psi_v(z^v_e)= {z'}^{\zeta(v)}_{\zeta(e)}</math> for every <math>v\in V^m</math> and adjacent edge <math>e\in E_v</math>; | ||
| Line 177: | Line 176: | ||
# Every edge <math>e\in E' = E</math> is labeled with the length <math>\ell_e:= \ell(\underline{\gamma}_e)\in[0,\infty]</math> of the associated generalized Morse trajectory. For the semi-infinite edges, this length is automatically <math>\ell_e=\infty</math> since the associated Morse trajectories are semi-infinite. | # Every edge <math>e\in E' = E</math> is labeled with the length <math>\ell_e:= \ell(\underline{\gamma}_e)\in[0,\infty]</math> of the associated generalized Morse trajectory. For the semi-infinite edges, this length is automatically <math>\ell_e=\infty</math> since the associated Morse trajectories are semi-infinite. | ||
# The domain for each vertex <math>v\in V'</math> is marked by <math>|v|</math> boundary points <math>\underline{z}_v=(z^v_e)_{e\in \{e^0_v\}\cup E^{\rm in}_v}\subset \partial D_v</math>, ordered counter-clockwise. | # The domain for each vertex <math>v\in V'</math> is marked by <math>|v|</math> boundary points <math>\underline{z}_v=(z^v_e)_{e\in \{e^0_v\}\cup E^{\rm in}_v}\subset \partial D_v</math>, ordered counter-clockwise. | ||
| − | # Two such trees are equivalent <math>[ (T, \underline{\ell} , \underline{z})]\sim [ (T', \underline{\ell}' , \underline{z}')]</math> if there is a tree isomorphism <math>\zeta:T\to T'</math> and a tuple of disk | + | # Two such trees are equivalent <math>[ (T, \underline{\ell} , \underline{z})]\sim [ (T', \underline{\ell}' , \underline{z}')]</math> if there is a tree isomorphism <math>\zeta:T\to T'</math> and a tuple of disk biholomorphisms <math>(\psi_v:D\to D)_{v\in V^m}</math> such that <math>\zeta</math> preserves the ordered tree structure and lengths <math>\ell_e=\ell'_{\zeta(e)}</math> for every <math>e\in E</math>, and the marked points are preserved <math>\psi_v(z^v_e)= z{'\;\zeta(v)}_{\zeta(e)}</math> for every <math>v\in V^m</math> and adjacent <math>e\in E</math>. |
</div> | </div> | ||
</div> | </div> | ||
| Line 193: | Line 192: | ||
We now expect the boundary stratification of the moduli spaces of disk trees <math>\mathcal{M}(x_0;x_1, \ldots, x_d)</math> - if/once regular - to arise exclusively from breaking of the Morse trajectories representing edges of the disk trees. This is made rigorous in [[https://math.berkeley.edu/~katrin/papers/disktrees.pdf J.Li thesis]] under the assumption that the almost complex structure <math>J</math> can be chosen such that there exist no nonconstant <math>J</math>-holomorphic spheres in the symplectic manifold <math>M</math>. | We now expect the boundary stratification of the moduli spaces of disk trees <math>\mathcal{M}(x_0;x_1, \ldots, x_d)</math> - if/once regular - to arise exclusively from breaking of the Morse trajectories representing edges of the disk trees. This is made rigorous in [[https://math.berkeley.edu/~katrin/papers/disktrees.pdf J.Li thesis]] under the assumption that the almost complex structure <math>J</math> can be chosen such that there exist no nonconstant <math>J</math>-holomorphic spheres in the symplectic manifold <math>M</math>. | ||
In that special case, all isotropy groups are trivial by [[https://math.berkeley.edu/~katrin/papers/disktrees.pdf Prop.2.5, J.Li thesis]]; that is any equivalence between a disk tree and itself, | In that special case, all isotropy groups are trivial by [[https://math.berkeley.edu/~katrin/papers/disktrees.pdf Prop.2.5, J.Li thesis]]; that is any equivalence between a disk tree and itself, | ||
| − | <math>(T, \underline{\gamma}, \underline{z}, \underline{u}) \sim (T, \underline{\gamma}, \underline{z}, \underline{u})</math>, is given by the trivial tree isomorphism <math>\zeta:T\to T</math>, and the only disk | + | <math>(T, \underline{\gamma}, \underline{z}, \underline{u}) \sim (T, \underline{\gamma}, \underline{z}, \underline{u})</math>, is given by the trivial tree isomorphism <math>\zeta:T\to T</math>, and the only disk biholomorphisms <math>(\psi_v:D\to D)_{v\in V^m}</math> which preserve the marked points and pseudoholomorphic disk maps are the identity maps <math>\psi_v={\rm id}_D</math>. |
In this case, the moduli spaces of disk trees <math>\mathcal{M}(x_0;x_1, \ldots, x_d)</math> are moreover Gromov-compact since sphere bubbling is ruled out and disk bubbling is captured by edges labeled with constant, zero length, Morse trajectories. | In this case, the moduli spaces of disk trees <math>\mathcal{M}(x_0;x_1, \ldots, x_d)</math> are moreover Gromov-compact since sphere bubbling is ruled out and disk bubbling is captured by edges labeled with constant, zero length, Morse trajectories. | ||
| Line 290: | Line 289: | ||
Finally, two pseudoholomorphic disk trees are equivalent <math>(T, \underline{\gamma}, \underline{z}, \underline{u} ) \sim (T', \underline{\gamma}', \underline{z}', \underline{u}')</math> if | Finally, two pseudoholomorphic disk trees are equivalent <math>(T, \underline{\gamma}, \underline{z}, \underline{u} ) \sim (T', \underline{\gamma}', \underline{z}', \underline{u}')</math> if | ||
<div class="toccolours mw-collapsible mw-collapsed"> | <div class="toccolours mw-collapsible mw-collapsed"> | ||
| − | there is a tree isomorphism <math>\zeta:T\to T'</math> and a tuple of disk | + | there is a tree isomorphism <math>\zeta:T\to T'</math> and a tuple of disk biholomorphisms <math>(\psi_v:D\to D)_{v\in V^m}</math> which preserve the tree, Morse trajectories, marked points, and pseudoholomorphic curves in the sense that |
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
* <math>\zeta</math> preserves the tree structure and order of edges; | * <math>\zeta</math> preserves the tree structure and order of edges; | ||
| − | |||
*<math>\underline{\gamma}_e=\underline{\gamma}'_{\zeta(e)}</math> for every <math>e\in E</math>; | *<math>\underline{\gamma}_e=\underline{\gamma}'_{\zeta(e)}</math> for every <math>e\in E</math>; | ||
* <math>\psi_v(z^v_e)= {z'}^{\zeta(v)}_{\zeta(e)}</math> for every <math>v\in V^m</math> and adjacent edge <math>e\in E_v</math>; | * <math>\psi_v(z^v_e)= {z'}^{\zeta(v)}_{\zeta(e)}</math> for every <math>v\in V^m</math> and adjacent edge <math>e\in E_v</math>; | ||
Revision as of 11:40, 28 May 2017
To construct the moduli spaces from which the composition maps are defined we fix an auxiliary almost complex structure  which is compatible with the symplectic structure in the sense that
which is compatible with the symplectic structure in the sense that  defines a metric on
defines a metric on  . (Unless otherwise specified, we will use this metric in all following constructions.)
. (Unless otherwise specified, we will use this metric in all following constructions.)
Then given Lagrangians  and generators
and generators 

 of their morphism spaces, we need to specify the Gromov-compactified moduli space
of their morphism spaces, we need to specify the Gromov-compactified moduli space  . (Here and throughout, we will call a moduli space Gromov-compact if its subsets of bounded symplectic area are compact in the Gromov topology.)
We will do this by combining two special cases which we discuss first.
. (Here and throughout, we will call a moduli space Gromov-compact if its subsets of bounded symplectic area are compact in the Gromov topology.)
We will do this by combining two special cases which we discuss first.
Pseudoholomorphic polygons for pairwise transverse Lagrangians
If each consecutive pair of Lagrangians is transverse,  , then our construction is based on pseudoholomorphic polygons
, then our construction is based on pseudoholomorphic polygons

where  is a disk with
is a disk with 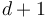 boundary punctures in counter-clockwise order
boundary punctures in counter-clockwise order  , and
, and  denotes the boundary component between
denotes the boundary component between  (resp. between
(resp. between  for i=d).
More precisely, we construct the (uncompactified) moduli spaces of pseudoholomorphic polygons for any tuple
for i=d).
More precisely, we construct the (uncompactified) moduli spaces of pseudoholomorphic polygons for any tuple  for
for  as in [Seidel book]:
as in [Seidel book]:

where
-
 is a tuple of pairwise disjoint marked points on the boundary of a disk, in counter-clockwise order.
is a tuple of pairwise disjoint marked points on the boundary of a disk, in counter-clockwise order. -
 is a smooth map satisfying
is a smooth map satisfying
- the Cauchy-Riemann equation
 ,
, - Lagrangian boundary conditions
 ,
, - the finite energy condition
 ,
, - the limit conditions
 for
for  .
.
- the Cauchy-Riemann equation
- The pseudoholomorphic polygon
 is stable in the sense that the map
is stable in the sense that the map  is nonconstant if the number of marked points is
is nonconstant if the number of marked points is  .
.
Here two pseudoholomorphic polygons are equivalent  if there is a biholomorphism
if there is a biholomorphism  that preserves the marked points
that preserves the marked points  , and relates the pseudoholomorphic polygons by reparametrization,
, and relates the pseudoholomorphic polygons by reparametrization,  .
.
The case  is not considered in this part of the moduli space setup since
is not considered in this part of the moduli space setup since  are never transverse. However, it might appear in the construction of homotopy units?
are never transverse. However, it might appear in the construction of homotopy units?
The domains of the pseudoholomorphic polygons are strips for  and represent elements in a Deligne-Mumford space for
and represent elements in a Deligne-Mumford space for 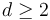 as follows:
as follows:
 are trivial; that is any disk biholomorphism
are trivial; that is any disk biholomorphism  that fixes
that fixes  marked points
marked points  , and preserves a pseudoholomorphic map
, and preserves a pseudoholomorphic map  must be the identity
must be the identity  .
. Next, to construct the Gromov-compactified moduli spaces  we have to add various strata to the moduli space of pseudoholomorphic polygons without breaking or nodes
we have to add various strata to the moduli space of pseudoholomorphic polygons without breaking or nodes  defined above.
defined above.
This is done precisely in the general construction below, but roughly requires to include breaking and bubbling, in particular
We will see that sphere bubbling does not contribute to the boundary stratification of these moduli spaces, so that the boundary stratification and thus the algebraic structure arising from these moduli spaces is induced by Floer breaking and disk bubbling. (On the other hand, sphere bubbling will be the only source of nontrivial isotropy.) The boundary strata arising from Floer breaking are fiber products of other moduli spaces of pseudoholomorphic polygons over finite sets of Lagrangian intersection points, which indicates an algebraic composition in this finitely generated Floer chain complex.
Disk bubbling, on the other hand, in the present setting yields boundary strata that are fiber products over the Lagrangian submanifold specified by the boundary condition, which is problematic for a combination of algebra and regularity reasons.
We will resolve this issue as in [J.Li thesis] by following another earlier proposal by Fukaya-Oh to allow disks to flow apart along a Morse trajectory, thus yielding disk trees which are constructed next - still ignoring sphere bubbling.
Pseudoholomorphic disk trees for a fixed Lagrangian
If the Lagrangians are all the same,  , then our construction is based on pseudoholomorphic disks
, then our construction is based on pseudoholomorphic disks

Such disks (modulo reparametrization by biholomorphisms of the disk) also arise from Gromov-compactifying other moduli spaces of pseudoholomorphic curves in which energy concentrates at a boundary point.
To capture this bubbling algebraically, we work throughout with the Morse function 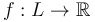 chosen in the setup of the morphism space
chosen in the setup of the morphism space  . We also choose a metric on
. We also choose a metric on  so that the gradient vector field
so that the gradient vector field  satisfies the Morse-Smale conditions and an additional technical assumption in [1] which guarantees a natural smooth manifold-with-boundary-and-corners structure on the compactified Morse trajectory spaces
satisfies the Morse-Smale conditions and an additional technical assumption in [1] which guarantees a natural smooth manifold-with-boundary-and-corners structure on the compactified Morse trajectory spaces
 for
for  .
This smooth structure is essentially induced by the requirement that the evaluation maps at positive and negative ends
.
This smooth structure is essentially induced by the requirement that the evaluation maps at positive and negative ends  are smooth.
With that data and the fixed almost complex structure
are smooth.
With that data and the fixed almost complex structure  we can construct the moduli spaces of pseudoholomorphic disk trees for any tuple
we can construct the moduli spaces of pseudoholomorphic disk trees for any tuple  as in JL:
as in JL:

where
1. 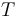 is an ordered tree with sets of vertices
is an ordered tree with sets of vertices  and edges
and edges  ,
,
equipped with orientations towards the root, orderings of incoming edges, and a partition into main and critical (leaf and root) vertices as follows:
2.  is a tuple of generalized Morse trajectories for each edge
is a tuple of generalized Morse trajectories for each edge
in the following compactified Morse trajectory spaces:
3.  is a tuple of boundary marked points for each main vertex
is a tuple of boundary marked points for each main vertex
that are ordered counter-clockwise as follows:
4.  is a tuple of pseudoholomorphic disks for each main vertex,
is a tuple of pseudoholomorphic disks for each main vertex,
that is each  is labeled by a smooth map
is labeled by a smooth map  satisfying
Cauchy-Riemann equation, Lagrangian boundary condition, finite energy, and matching conditions as follows:
satisfying
Cauchy-Riemann equation, Lagrangian boundary condition, finite energy, and matching conditions as follows:
5. The disk tree is stable
in the sense that
Finally, two pseudoholomorphic disk trees are equivalent  if
if
there is a tree isomorphism  and a tuple of disk biholomorphisms
and a tuple of disk biholomorphisms  which preserving the tree, Morse trajectories, marked points, and pseudoholomorphic curves in the sense that
which preserving the tree, Morse trajectories, marked points, and pseudoholomorphic curves in the sense that
The domains of the disk trees are never stable for  , but need to be studied to construct the
differential
, but need to be studied to construct the
differential  on the Floer chain complex and the curvature term
on the Floer chain complex and the curvature term  that may obstruct
that may obstruct  .
For
.
For 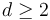 the domains of the disk trees represent elements in a Deligne-Mumford space as follows:
the domains of the disk trees represent elements in a Deligne-Mumford space as follows:
We now expect the boundary stratification of the moduli spaces of disk trees  - if/once regular - to arise exclusively from breaking of the Morse trajectories representing edges of the disk trees. This is made rigorous in [J.Li thesis] under the assumption that the almost complex structure
- if/once regular - to arise exclusively from breaking of the Morse trajectories representing edges of the disk trees. This is made rigorous in [J.Li thesis] under the assumption that the almost complex structure  can be chosen such that there exist no nonconstant
can be chosen such that there exist no nonconstant  -holomorphic spheres in the symplectic manifold
-holomorphic spheres in the symplectic manifold  .
In that special case, all isotropy groups are trivial by [Prop.2.5, J.Li thesis]; that is any equivalence between a disk tree and itself,
.
In that special case, all isotropy groups are trivial by [Prop.2.5, J.Li thesis]; that is any equivalence between a disk tree and itself,
 , is given by the trivial tree isomorphism
, is given by the trivial tree isomorphism  , and the only disk biholomorphisms
, and the only disk biholomorphisms  which preserve the marked points and pseudoholomorphic disk maps are the identity maps
which preserve the marked points and pseudoholomorphic disk maps are the identity maps  .
In this case, the moduli spaces of disk trees
.
In this case, the moduli spaces of disk trees  are moreover Gromov-compact since sphere bubbling is ruled out and disk bubbling is captured by edges labeled with constant, zero length, Morse trajectories.
are moreover Gromov-compact since sphere bubbling is ruled out and disk bubbling is captured by edges labeled with constant, zero length, Morse trajectories.
In general, we will Gromov-compactify  in the following general construction by allowing for sphere bubble trees developing at any (boundary or interior) point of each of the disk domains. This will also be a source of generally nontrivial isotropy.
in the following general construction by allowing for sphere bubble trees developing at any (boundary or interior) point of each of the disk domains. This will also be a source of generally nontrivial isotropy.
General moduli space of pseudoholomorphic polygons
For the construction of a general  -composition map we are given
-composition map we are given  Lagrangians
Lagrangians  and a fixed autonomous Hamiltonian function
and a fixed autonomous Hamiltonian function  for each pair
for each pair  whose time-1 flow provides transverse intersections
whose time-1 flow provides transverse intersections  .
To simplify notation for consecutive Lagrangians in the list, we index it cyclically by
.
To simplify notation for consecutive Lagrangians in the list, we index it cyclically by  and abbreviate
and abbreviate  so that we have
so that we have  whenever
whenever  , and in particular
, and in particular  unless
unless  .
Now, given generators
.
Now, given generators  of these morphism spaces, we construct the Gromov-compactified moduli space of pseudoholomorphic polygons by combining the two special cases above:
of these morphism spaces, we construct the Gromov-compactified moduli space of pseudoholomorphic polygons by combining the two special cases above:
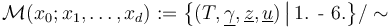
where
1. 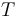 is an ordered tree with sets of vertices
is an ordered tree with sets of vertices  and edges
and edges  ,
,
equipped with orientations towards the root, orderings of incoming edges, and a partition into main and critical (leaf and root) vertices as follows:
2. The tree structure induces tuples of Lagrangians 
that label the boundary components of domains in overall counter-clockwise order  as follows:
as follows:
3.  is a tuple of generalized Morse trajectories
is a tuple of generalized Morse trajectories
in the following compactified Morse trajectory spaces:
4.  is a tuple of boundary points
is a tuple of boundary points
that are ordered counter-clockwise and associate complex domains  to the vertices as follows:
to the vertices as follows:
5.  is a tuple of pseudoholomorphic maps for each main vertex,
is a tuple of pseudoholomorphic maps for each main vertex,
that is each  is labeled by a smooth map
is labeled by a smooth map  satisfying Cauchy-Riemann equation, Lagrangian boundary conditions, finite energy, and matching conditions as follows:
satisfying Cauchy-Riemann equation, Lagrangian boundary conditions, finite energy, and matching conditions as follows:
6. The disk tree is stable
in the sense that
Finally, two pseudoholomorphic disk trees are equivalent  if
if
there is a tree isomorphism  and a tuple of disk biholomorphisms
and a tuple of disk biholomorphisms  which preserve the tree, Morse trajectories, marked points, and pseudoholomorphic curves in the sense that
which preserve the tree, Morse trajectories, marked points, and pseudoholomorphic curves in the sense that
NOTE: when degenerating polygons to create a strip with  boundary conditions, will need to transfer from Morse-Bott breaking to boundary node
boundary conditions, will need to transfer from Morse-Bott breaking to boundary node
Finally, the symplectic area function  in each case is given by TODO
in each case is given by TODO
Fredholm index 
![\Sigma _{{\{z_{0},z_{1}\}}}\simeq \mathbb{R} \times [0,1]](/images/math/8/b/3/8b3c9f4dfa661a678858f5301011005f.png) , so that we could equivalently set up the moduli spaces
, so that we could equivalently set up the moduli spaces  by fixing the domain
by fixing the domain ![\Sigma _{{d=1}}:=\mathbb{R} \times [0,1]](/images/math/b/9/b/b9b8b4c742fe7b67774c1dfe2eb02833.png) and defining the equivalence relation
and defining the equivalence relation  only in terms of the shift action
only in terms of the shift action  of
of  . This is the only case in which the stability condition is nontrivial: It requires the maps
. This is the only case in which the stability condition is nontrivial: It requires the maps ![u:\mathbb{R} \times [0,1]\to M](/images/math/3/9/e/39e5527f65a10854493238103878da42.png) to be nonconstant.
to be nonconstant.

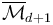 , whose boundary and corner strata can be represented by trees of polygonal domains
, whose boundary and corner strata can be represented by trees of polygonal domains  with each edge
with each edge  represented by two punctures
represented by two punctures  and
and  . The thin neighbourhoods of these punctures are biholomorphic to half-strips, and a neighbourhood of a tree of polygonal domains is obtained by gluing the domains together at the pairs of strip-like ends represented by the edges.
. The thin neighbourhoods of these punctures are biholomorphic to half-strips, and a neighbourhood of a tree of polygonal domains is obtained by gluing the domains together at the pairs of strip-like ends represented by the edges.
 this follows directly from the marked points, since any Mobius transformation that fixes three points is the identity.
this follows directly from the marked points, since any Mobius transformation that fixes three points is the identity.
 .
On the other hand, any J-holomorphic map
.
On the other hand, any J-holomorphic map  with
with  .
If we now had nontrivial isotropy, i.e.
.
If we now had nontrivial isotropy, i.e.  for some
for some  and a nonconstant map
and a nonconstant map  , then there would exist
, then there would exist ![s_{0},t_{0}\in \mathbb{R} \times [0,1]](/images/math/4/a/5/4a585dfca885c55d7af17fbe38e8de85.png) with
with  and thus
and thus
![\textstyle \int _{{[s_{0}-{\frac {1}{2}}\tau ]\times [0,1]}}^{{[s_{0}+{\frac {1}{2}}\tau ]\times [0,1]}}u^{*}\omega >0](/images/math/4/c/0/4c0d3fcb1b294a69a84d18c923afba12.png) .
However, this is in contradiction to
.
However, this is in contradiction to ![\infty >\textstyle \int _{{\mathbb{R} \times [0,1]}}u^{*}\omega =\sum _{{k\in \mathbb{Z } }}\int _{{[s_{0}+(k-{\frac {1}{2}})\tau ]\times [0,1]}}^{{[s_{0}+(k+{\frac {1}{2}})\tau ]\times [0,1]}}u^{*}\omega =\sum _{{k\in \mathbb{Z } }}\int _{{[s_{0}-{\frac {1}{2}}\tau ]\times [0,1]}}^{{[s_{0}+{\frac {1}{2}}\tau ]\times [0,1]}}u^{*}\omega .](/images/math/5/6/5/56523b116cf68bcb2660fce82a153701.png)
 whose domain is a nontrivial tree of domains
whose domain is a nontrivial tree of domains ![[(\Sigma _{v})_{{v\in V}},(z_{e}^{\pm })_{{e\in E}}]\in \overline {\mathcal {M}}_{{d+1}}](/images/math/8/b/6/8b69080d370c68dbb8f70d2174ba64b5.png) ;
; , i.e. a finite string of pseudoholomorphic strips in
, i.e. a finite string of pseudoholomorphic strips in  ;
; are oriented towards the root vertex
are oriented towards the root vertex  of the tree, i.e. for
of the tree, i.e. for  the outgoing vertex
the outgoing vertex  is still connected to the root after removing
is still connected to the root after removing  . Thus each vertex
. Thus each vertex  has a unique outgoing edge
has a unique outgoing edge  (except for the root vertex which has no outgoing edge) and a (possibly empty) set of incoming edges
(except for the root vertex which has no outgoing edge) and a (possibly empty) set of incoming edges  . Moreover, the set of incoming edges is ordered,
. Moreover, the set of incoming edges is ordered,  with
with  denoting the valence - number of attached edges - of
denoting the valence - number of attached edges - of  .
.  into the sets of main vertices
into the sets of main vertices  and the set of critical vertices
and the set of critical vertices  . The latter is ordered to start with the root
. The latter is ordered to start with the root  , which is required to have a single edge
, which is required to have a single edge  , and then contains d leaves
, and then contains d leaves  of the tree (i.e. with
of the tree (i.e. with  ), with order induced by the orientation and order of the edges (with the root being the minimal vertex).
), with order induced by the orientation and order of the edges (with the root being the minimal vertex). for any edge
for any edge  between critical vertices;
between critical vertices; for any edge
for any edge  from a critical vertex
from a critical vertex  ;
; for any edge
for any edge  from a main vertex
from a main vertex  ;
; for any edge
for any edge  .
. on the boundary of a disk.
on the boundary of a disk.  of the edges corresponds to a counter-clockwise order of the marked points
of the edges corresponds to a counter-clockwise order of the marked points  .
. and
and  by the edges
by the edges  .
. .
. .
. and
and  by the edges
by the edges  whenever
whenever  .
. (which is equivalent to
(which is equivalent to  being constant) has valence
being constant) has valence  .
.
 preserves the tree structure and order of edges;
preserves the tree structure and order of edges;  for every
for every  ;
; for every
for every  ;
; for every
for every ![[(T,\underline {\gamma },\underline {z},\underline {u})]](/images/math/3/8/3/383800ad42d3c5072e12f54b0a6fe3f9.png) induces a domain tree
induces a domain tree ![[(T',\underline {\ell },\underline {z})]](/images/math/d/4/1/d41dd318d5fd7a04cf8aa75ae103c19e.png)
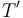 is obtained from
is obtained from  of
of  .
.  is labeled with the length
is labeled with the length ![\ell _{e}:=\ell (\underline {\gamma }_{e})\in [0,\infty ]](/images/math/5/c/0/5c00882bd14859421d79bd58c855a5d3.png) of the associated generalized Morse trajectory. For the semi-infinite edges, this length is automatically
of the associated generalized Morse trajectory. For the semi-infinite edges, this length is automatically  since the associated Morse trajectories are semi-infinite.
since the associated Morse trajectories are semi-infinite. is marked by
is marked by  , ordered counter-clockwise.
, ordered counter-clockwise. ![[(T,\underline {\ell },\underline {z})]\sim [(T',\underline {\ell }',\underline {z}')]](/images/math/b/a/2/ba206065fa9403003359115ed475c49e.png) if there is a tree isomorphism
if there is a tree isomorphism  for every
for every  for every
for every  .
The domain trees for
.
The domain trees for  is constructed by counting the elements of
is constructed by counting the elements of  with no incoming critical points, serves to algebraically encode disk bubbling in any moduli space involving a Lagrangian boundary condition on
with no incoming critical points, serves to algebraically encode disk bubbling in any moduli space involving a Lagrangian boundary condition on  in the sense of [
in the sense of [ by a single edge
by a single edge  of length
of length  . The space of such stable rooted metric ribbon trees - where a tree containing an edge of length
. The space of such stable rooted metric ribbon trees - where a tree containing an edge of length  is identified with the tree in which this edge and its adjacent vertices are replaced by a single vertex - is another topological representation of the
is identified with the tree in which this edge and its adjacent vertices are replaced by a single vertex - is another topological representation of the  adjacent to
adjacent to  , and we will denote consecutive edges in this order by
, and we will denote consecutive edges in this order by  . In particular this yields
. In particular this yields  .
.  has a single edge
has a single edge  , and this attaches to a main vertex
, and this attaches to a main vertex  between its two critical vertices
between its two critical vertices  .
.  is a cyclic sequence of Lagrangians
is a cyclic sequence of Lagrangians  indexed by the adjacent edges
indexed by the adjacent edges  (which will become the boundary condition on
(which will become the boundary condition on  ).
). the Lagrangian labels satisfy a matching condition as follows:
the Lagrangian labels satisfy a matching condition as follows:
 requires
requires  .
. requires
requires  .
. requires
requires  and
and  .
. if
if  , resp. by the constant
, resp. by the constant  in the discrete space
in the discrete space  if
if  attaches to a main vertex
attaches to a main vertex  if
if  in the discrete space
in the discrete space  if
if  .
. and the tree with one edge
and the tree with one edge  in case
in case  , resp. by a constant
, resp. by a constant  in the discrete space
in the discrete space  in case
in case  . (Recall the matching condition
. (Recall the matching condition  and
and  from 2.)
from 2.) on the boundary of a disk.
on the boundary of a disk.  of the edges corresponds to a counter-clockwise order of the marked points
of the edges corresponds to a counter-clockwise order of the marked points  partition the boundary into
partition the boundary into  such that the closure of each component
such that the closure of each component  .
.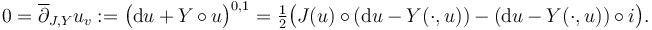
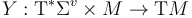 is a vector-field-valued 1-form on
is a vector-field-valued 1-form on  that is chosen compatibly with the fixed Hamiltonian perturbations as follows:
that is chosen compatibly with the fixed Hamiltonian perturbations as follows:
![\iota _{e}^{v}:(-\infty ,0)\times [0,1]\hookrightarrow \Sigma ^{v}](/images/math/b/3/5/b35893c49e2a7b041f97659155347357.png) near each puncture
near each puncture  we have
we have 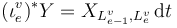 .
.
 in case
in case 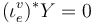 in case
in case  .
.
 ; more precisely this requires
; more precisely this requires  for each adjacent edge
for each adjacent edge  .
.  associated to the edge
associated to the edge  , that is
, that is  for
for  .
.  , the map
, the map ![u_{e}^{v}:=(\iota _{e}^{v})^{*}u_{v}:(-\infty ,0)\times [0,1]\to M](/images/math/6/3/7/63792330def3bf1b30267f5afb4d519f.png) has a uniform limit
has a uniform limit  for some
for some  , and this limit intersection point is required to match with the value of the constant 'Morse trajectory'
, and this limit intersection point is required to match with the value of the constant 'Morse trajectory'  associated to the edge
associated to the edge  .
.