Difference between revisions of "Polyfold constructions for Fukaya categories"

From Polyfolds.org
Jump to: navigation, search
(→‎Morphisms)
(→‎Morphisms)
Line 25: Line 25:
 
<math>{\mathbb K}=\Q</math> or <math>{\mathbb K}=\Z_2</math>,  
 
<math>{\mathbb K}=\Q</math> or <math>{\mathbb K}=\Z_2</math>,  
 
<center>
 
<center>
−
<math>\Lambda = \{ \sum_{i=0}^\infty a_i T^{\lambda_i} \,|\, a_i\in \mathbb{K}, \R\ni \lambda_i \undereset {i\to\infty}{\to} \infty\}</math>
+
<math>\Lambda = \{ \sum_{i=0}^\infty a_i T^{\lambda_i} \,|\, a_i\in \mathbb{K}, \R\ni \lambda_i \underset {i\to\infty}{\to} \infty\}</math>
 
</center>
 
</center>
  

Revision as of 12:27, 20 May 2017


Fukaya categories capture the chain level information contained in Lagrangian Floer theory and its product structures. For an introduction see e.g. Auroux' Beginner's introduction to Fukaya categories [1].

There are different constructions (and even more proposals) depending on the properties of the (fixed) ambient symplectic manifold. For example, Seidel [2] considers exact symplectic manifolds and constructs an (uncurved) Fukaya 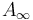A_{\infty } category whose objects are exact Lagrangians (with a brane structure), whose morphism spaces are Floer complexes (depending on the choice of a Hamiltonian), and whose composition operations are given by counting pseudoholomorphic polygons with boundary on the Lagrangians. (Here the benefit of the exactness assumption is that bubbling is excluded, so that the moduli spaces can be regularized by geometric methods (choices of Hamiltonian perturbations and almost complex structures). On the other hand, exact symplectic manifolds (on which the symplectic 2-form is exact) are necessarily noncompact, so one needs to assume certain boundedness and convexity conditions to ensure that pseudoholomorphic curves do not escape to infinity.)

This wiki will focus on the main difficulty that is not addressed in Seidel's book: How to regularize the moduli spaces of pseudoholomorphic polygons when geometric methods fail (e.g. due to sphere bubbling), and how to capture disk bubbling algebraically. To limit the classical analytic challenges in studying the pseudoholomorphic curves involved, we restrict our constructions to a fixed compact symplectic manifold 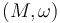(M,\omega ). Then the Fukaya category of M consists of the following data:

Objects

The Objects of 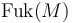\operatorname {Fuk}(M) are - roughly speaking - the compact Lagrangian submanifolds 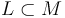L\subset M. More precisely, each object is a Lagrangian equipped with a brane structure.

Here input from the Mirror Symmetry community is needed to determine what specific brane structures should be used. For the time being, we will treat brane structures as abstract gadgets that induce gradings on Floer or Morse complexes (which will form the morphism spaces) and orientations on the moduli spaces of pseudoholomorphic curves (from which we will construct the composition maps).

For special symplectic manifolds (those equipped with an almost complex structure J for which all J-holomorphic spheres are constant) we could work with Lagrangians without additional brane structure. In this case of trivial brane structures we will not have gradings or orientations, and thus will have to work with 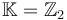{{\mathbb K}}={{\mathbb Z}}_{2} coefficients in the following.

Morphisms

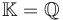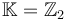The morphism spaces of an A_{\infty }-category forms a graded vector space over a field. For Fukaya categories this typically is the Novikov field over a fixed field {{\mathbb K}} such as {{\mathbb K}}=\mathbb{Q} or {{\mathbb K}}=\mathbb{Z } _{2},

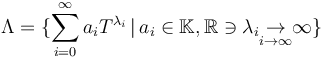
\Lambda =\{\sum _{{i=0}}^{\infty }a_{i}T^{{\lambda _{i}}}\,|\,a_{i}\in {\mathbb {K}},\mathbb{R} \ni \lambda _{i}{\underset {i\to \infty }{\to }}\infty \}

Moreover, we denote the coefficient system by {{\mathbb K}} and assume for the time being that it is given by a constant field.

For two Lagrangians 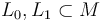L_{0},L_{1}\subset M that are transverse (i.e. 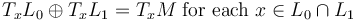T_{x}L_{0}\oplus T_{x}L_{1}=T_{x}M\;{\text{for each}}\;x\in L_{0}\cap L_{1}) and hence have a finite set of intersection points, the natural choice of morphism space is

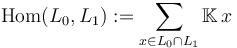{\text{Hom}}(L_{0},L_{1}):=\sum _{{x\in L_{0}\cap L_{1}}}{\mathbb {K}}\,x.

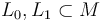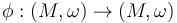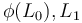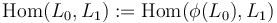When L_{0},L_{1}\subset M are not transverse, then we will choose a Hamiltonian symplectomorphism \phi :(M,\omega )\to (M,\omega ) such that \phi (L_{0}),L_{1} are transverse, and define {\text{Hom}}(L_{0},L_{1}):={\text{Hom}}(\phi (L_{0}),L_{1}).


When considering the isomorphism space 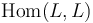{\text{Hom}}(L,L) of a fixed Lagrangian 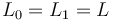L_{0}=L_{1}=L, then the Hamiltonian symplectomorphism 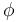\phi can be obtained by lifting a Morse function 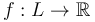f:L\to \mathbb{R} to a Hamiltonian function in a neighborhood 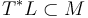T^{*}L\subset M. After extending it suitably, the intersection points can be identified with the critical points, 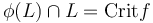\phi (L)\cap L={\text{Crit}}f. Thus in this case we define

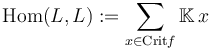{\text{Hom}}(L,L):=\sum _{{x\in {\text{Crit}}f}}{{\mathbb K}}\,x.

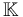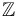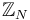Each of the sets of homomorphisms defined above is a vector space over the field {{\mathbb K}}. For most versions of Fukaya categories, these vector spaces should also be graded over {{\mathbb Z}} or {{\mathbb Z}}_{N}. This grading will arise from additional data in the brane structure for each Lagrangian.


Here the choice of the Morse complex for the isomorphism spaces is based on input from the Mirror Symmetry community. Further input is needed to decide how to track or deal with these choices algebraically, and which exact gradings to use - depending on the desired brane structures.

Composition Operations

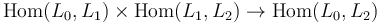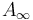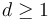While a category has a single composition map {\text{Hom}}(L_{0},L_{1})\times {\text{Hom}}(L_{1},L_{2})\to {\text{Hom}}(L_{0},L_{2}), an A_{\infty }-category has composition maps of every order d\geq 1,

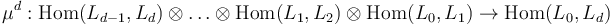
\mu ^{d}:{\text{Hom}}(L_{{d-1}},L_{d})\otimes \ldots \otimes {\text{Hom}}(L_{1},L_{2})\otimes {\text{Hom}}(L_{0},L_{1})\to {\text{Hom}}(L_{0},L_{d})

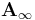{\mathbf {A}}_{{\mathbf {\infty }}}-Relations

Invariance

Retrieved from "http://www.polyfolds.org/index.php?title=Polyfold_constructions_for_Fukaya_categories&oldid=94"