Moduli spaces of pseudoholomorphic polygons

To construct the moduli spaces from which the composition maps are defined we fix an auxiliary almost complex structure $J:TM\to TM$ which is compatible with the symplectic structure in the sense that $\omega (\cdot ,J\cdot )$ defines a metric on $M$. (Unless otherwise specified, we will use this metric in all following constructions.) Then given Lagrangians $L_{0},\ldots ,L_{d}\subset M$ and generators $x_{0}\in {\text{Crit}}(L_{0},L_{d}),x_{1}\in {\text{Crit}}(L_{0},L_{1}),\ldots ,x_{d}\in {\text{Crit}}(L_{{d-1}},L_{d})$ of their morphism spaces, we need to specify the moduli space $\overline {\mathcal {M}}(x_{0};x_{1},\ldots ,x_{d})$. We will do this below by combining two special cases.

Disk trees for a fixed Lagrangian

If the Lagrangians are all the same, $L_{0}=L_{1}=\ldots =L_{d}=:L$, then our construction is based on pseudoholomorphic disks

$u:D\to M,\qquad u(\partial D)\subset L,\qquad \overline \partial _{J}u=0.$

Pseudoholomorphic polygons for pairwise transverse Lagrangians

If each consecutive pair of Lagrangians is transverse, i.e. $L_{0}\pitchfork L_{1},L_{1}\pitchfork L_{2},\ldots ,L_{{d-1}}\pitchfork L_{d},L_{d}\pitchfork L_{0}$, then our construction is based on pseudoholomorphic polygons

$u:\Sigma \to M,\qquad u((\partial \Sigma )_{i})\subset L_{i},\qquad \overline \partial _{J}u=0,$

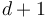where $\Sigma =D\setminus \{z_{0},\ldots ,z_{d}\}$ is a disk with $d+1$ boundary punctures in counter-clockwise order $z_{0},\ldots ,z_{d}\subset \partial D$, and $(\partial \Sigma )_{i}$ denotes the boundary component between $z_{i},z_{{i+1}}$ (resp. between $z_{{d}},z_{0}$ for i=d).

General moduli space of pseudoholomorphic polygons

Make up for differences in Hamiltonian symplectomorphisms applied to each Lagrangian by a domain-dependent Hamiltonian perturbation to the Cauchy-Riemann equation

Finally, the symplectic area function $\omega :\overline {\mathcal {M}}(x_{0};x_{1},\ldots ,x_{d})\to \mathbb{R}$ in each case is given by TODO