Deligne-Mumford space
From Polyfolds.org
Revision as of 09:08, 24 May 2017 by Katrin (Talk | contribs) (Created page with "table of contents '''TODO:''' Expand on this copy of a sketch in the moduli space construction For <math>d\geq 2</math>, the moduli space of domains <center><math> \math...")
TODO: Expand on this copy of a sketch in the moduli space construction
For 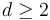 , the moduli space of domains
, the moduli space of domains

can be compactified to form the Deligne-Mumford space  , whose boundary and corner strata can be represented by trees of polygonal domains
, whose boundary and corner strata can be represented by trees of polygonal domains  with each edge
with each edge  represented by two punctures
represented by two punctures  and
and  . The thin neighbourhoods of these punctures are biholomorphic to half-strips, and then a neighbourhood of a tree of polygonal domains is obtained by gluing the domains together at the pairs of strip-like ends represented by the edges.
. The thin neighbourhoods of these punctures are biholomorphic to half-strips, and then a neighbourhood of a tree of polygonal domains is obtained by gluing the domains together at the pairs of strip-like ends represented by the edges.