Deligne-Mumford space

table of contents

TODO: Expand on this copy of a sketch in the moduli space construction

For 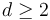$d\geq 2$, the moduli space of domains

${\mathcal {M}}_{{d+1}}:={\frac {{\bigl \{}\Sigma _{{\underline {z}}}\,{\big |}\,\underline {z}=\{z_{0},\ldots ,z_{d}\}\in \partial D\;{\text{pairwise disjoint}}{\bigr \}}}{\Sigma _{{\underline {z}}}\sim \Sigma _{{\underline {z}'}}\;{\text{iff}}\;\exists \psi :\Sigma _{{\underline {z}}}\to \Sigma _{{\underline {z}'}},\;\psi ^{*}i=i}}$

can be compactified to form the Deligne-Mumford space 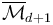$\overline {\mathcal {M}}_{{d+1}}$, whose boundary and corner strata can be represented by trees of polygonal domains $(\Sigma _{v})_{{v\in V}}$ with each edge $e=(v,w)$ represented by two punctures $z_{e}^{-}\in \Sigma _{v}$ and $z_{e}^{+}\in \Sigma _{w}$. The thin neighbourhoods of these punctures are biholomorphic to half-strips, and then a neighbourhood of a tree of polygonal domains is obtained by gluing the domains together at the pairs of strip-like ends represented by the edges.

The space of stable rooted metric ribbon trees, as discussed in [BV], is another topological representation of the (compactified) Deligne Mumford space 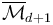$\overline {\mathcal {M}}_{{d+1}}$.