Problems on Deligne-Mumford spaces
From Polyfolds.org
Revision as of 14:52, 26 May 2017 by Natebottman (Talk | contribs)
poset underlying associahedra
As described in Deligne-Mumford space, for any 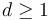 ,
, 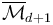 is a
is a  -dimensional manifold with boundary and corners which parametrizes nodal trees of disks with
-dimensional manifold with boundary and corners which parametrizes nodal trees of disks with 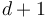 marked points, one of them distinguished (we think of the
marked points, one of them distinguished (we think of the 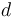 undistinguished resp. 1 distinguished marked points as "input" resp. "output" marked points).
As shown in [Auroux, Ex. 2.6],
undistinguished resp. 1 distinguished marked points as "input" resp. "output" marked points).
As shown in [Auroux, Ex. 2.6], 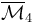 is homeomorphic to a closed interval, with one endpoint corresponding to a collision of the first two inputs
is homeomorphic to a closed interval, with one endpoint corresponding to a collision of the first two inputs 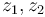 and the other corresponding to a collision of
and the other corresponding to a collision of 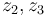 .
Work out which polygon/polyhedron
.
Work out which polygon/polyhedron  are equal to.
are equal to.