Regularized moduli spaces

table of contents

WORK IN PROGRESS

In order to regularize the moduli spaces of pseudoholomorphic polygons $\overline {\mathcal {M}}(x_{0};x_{1},\ldots ,x_{d})$ for each tuple of Lagrangians $\underline {L}={\bigl (}L_{0},\ldots ,L_{d}\subset M{\bigr )}$, generators $\underline {x}={\bigl (}x_{0}\in {\text{Crit}}(L_{0},L_{d}),x_{1}\in {\text{Crit}}(L_{0},L_{1}),\ldots ,x_{d}\in {\text{Crit}}(L_{{d-1}},L_{d}){\bigr )}$, and a fixed compatible almost complex structure $J$, any abstract regularization approach (opposed to geometric ones, as contrasted in [section 3, FFGW] and [sections 2.1-2, McDuff-Wehrheim]) starts by describing each Gromov-compactified moduli space as

${\text{zero set}}\quad \overline {\mathcal {M}}(x_{0};x_{1},\ldots ,x_{d})=\overline \partial _{{J,Y}}^{{-1}}(0)\quad {\text{of a section}}\quad \overline \partial _{{J,Y}}:{\mathcal {X}}(\underline {x})\to {\mathcal {Y}}(\underline {x},J)\quad {\text{of a bundle}}\quad \pi :{\mathcal {Y}}(\underline {x},J)\to {\mathcal {X}}(\underline {x}).$

In order to obtain boundary stratifications which imply the 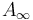$A_{\infty }$-relations, any abstract approach needs to regularize ‘’coherently’’ (whereas geometric regularizations are automatically coherent), that is compatible with the boundary stratification of the ambient spaces ${\mathcal {X}}(\underline {x})$ being given by fiber products of other ambient spaces. In our setup, these fiber products are over finite sets of Morse and Floer critical points, so simplify to unions of Cartesian products,

$\partial {\mathcal {X}}(x_{0};x_{1},\ldots ,x_{d})=\bigsqcup _{{m,n\geq 0}}\bigsqcup _{{y\in {\text{Crit}}(L_{n},L_{{m+n}})}}{\mathcal {X}}(y;\underline {x}')\times {\mathcal {X}}(x_{0};\underline {x},y,\underline {x}''),$

with $\underline x=(x_{1},\ldots ,x_{n}),\underline {x}'=(x_{{n+1}},\ldots ,x_{{n+m}}),\underline {x}''=(x_{{n+m+1}},\ldots ,x_{d}),$

[Expand]

In the abstract regularization approach of [2015-FOOO1], [2017-FOOO2], and most other virtual approaches, the global sections $s:{\mathcal {Y}}\to {\mathcal {X}}$ are patched together from smooth sections of finite rank bundles over finite dimensional manifolds $s_{i}:Y_{i}\to X_{i}$. While at first glance this resolves most analytic issues (up to the question of how to actually obtain smooth sections near nodal curves from the classical gluing analysis), it introduces a number of subtle combinatorial, algebraic, and topological challenges as discussed in [McDuff-Wehrheim].

Many of these challenges stem from the lack of a natural ambient space, which is replaced by a highly choice-dependent space ${\mathcal {X}}$ that is constructed from nontrivial notions of transition data between the local base manifolds $X_{i}$ of different dimensions. Other undesirable features of this approach are that the sections $s_{i}$ are no longer directly identified with Cauchy-Riemann operators, and that the Kuranishi charts $s_{i}:Y_{i}\to X_{i}$ are generally 'too small' to allow for straight-forward constructions of new moduli spaces (e.g. by restriction to curves having certain intersection properties, or coupling of curves with each other or Morse trajectories) via restrictions or fiber products of the local sections. (Such constructions require transversality of evaluation maps whose domain is the ambient space ${\mathcal {X}}$, which would need to be constructed with the particular transversality in mind.)

In the abstract regularization approach via polyfold theory TODO: links to papers, the ambient space ${\mathcal {X}}$ is chosen ‘large enough’ to be fairly natural, allow for restrictions and fiber products, and so that the section $\overline \partial _{{J,Y}}$ is directly given by a Cauchy-Riemann operator. While this resolves most combinatorial, algebraic, and topological challenges - by building a natural ambient space that is e.g. Hausdorff and provides natural compactness controls - introducing a notion of smooth structure

analytic issues

we will provide Polyfold Fredholm descriptions for them - as

---

[Expand]

talk about Fredholm index $\overline {\mathcal {M}}^{k}(\ldots )=\{b\in {\mathcal {M}}(\ldots )\,|\,IND...=k\}$

we need to explain how to obtain regularizations $\overline {\mathcal {M}}^{k}(x_{0};x_{1},\ldots ,x_{d};\nu )$ for expected dimensions $k=0,1$ by a choice of perturbations $\nu$. Moreover, we need to choose these perturbations coherently to ensure that the boundary of each 1-dimensional part is given by Cartesian products of 0-dimensional parts,

$\partial \overline {\mathcal {M}}^{1}(x_{0};x_{1},\ldots ,x_{d};\nu )=\bigsqcup _{{m,n\geq 0}}\bigsqcup _{{y\in {\text{Crit}}(L_{n},L_{{m+n}})}}\overline {\mathcal {M}}^{0}(y;\underline {x}';\nu )\times \overline {\mathcal {M}}^{0}(x_{0};\underline {x},y,\underline {x}'';\nu ).$

Finally, we need to check that for each pair $(b,b')\in \overline {\mathcal {M}}^{0}(x_{0};\underline {x},y,\underline {x}'';\nu )\times \overline {\mathcal {M}}^{0}(y;\underline {x}';\nu )$, when considered as boundary point $(b,b')\in \partial \overline {\mathcal {M}}^{1}(x_{0};x_{1},\ldots ,x_{d};\nu )$, has symplectic area $\omega ((b,b'))=\omega (b)+\omega (b')$ and weight function ${\text{w}}((b,b'))=(-1)^{{\|\underline x\|}}{\text{w}}(b){\text{w}}(b')$.

---

---

[Expand]

Analysis TODO:

when degenerating polygons to create a strip with $L_{i}=L_{j}$ boundary conditions, will need to transfer from Morse-Bott breaking to boundary node