Ambient space

table of contents

This section constructs topological ambient spaces ${\mathcal {X}}(\underline {x})$ of the moduli spaces of pseudoholomorphic polygons $\overline {\mathcal {M}}(\underline {x})=\overline \partial _{{J,Y}}^{{-1}}(0)$, within which polyfold theory will construct the regularized moduli spaces $\overline {\mathcal {M}}(\underline {x};\nu )$. These will depend only on the choice of a Sobolev decay constant $\delta >0$.

Thus we are given $d+1\geq 1$ Lagrangians $L_{0},\ldots ,L_{d}\subset M$ (indexed cyclically by $i\in \mathbb{Z } _{{d+1}}$) and generators $x_{0}\in {\text{Crit}}(L_{0},L_{d}),$ $x_{1}\in {\text{Crit}}(L_{0},L_{1}),\ldots ,$ $x_{d}\in {\text{Crit}}(L_{{d-1}},L_{d})$ of their morphism spaces. The latter depend on the choice of Hamiltonian symplectomorphisms $\phi _{i}:=\phi _{{L_{{i-1}},L_{i}}}$ so that we have $\phi _{i}(L_{{i-1}})\pitchfork L_{i}$ whenever $L_{{i-1}}\neq L_{i}$, as specified in polyfold constructions for Fukaya categories and moduli spaces of pseudoholomorphic polygons.

Then - as set - we define the ambient space as

${\mathcal {X}}(x_{0};x_{1},\ldots ,x_{d}):={\bigl \{}(T,\underline {\gamma },\underline {z},\underline {w},\underline {\beta },\underline {u})\,{\big |}\,{\text{1. - 8.}}{\bigr \}}/\sim$

where the data is the same as in the construction of the moduli spaces of pseudoholomorphic polygons $\overline {\mathcal {M}}(\underline {x})$, except for maps not necessarily being pseudoholomorphic but just of Sobolev $H^{{3,\delta }}$-regularity. We indicate these differences in boldface.

1. 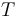$T$ is an ordered tree with sets of vertices $V=V^{m}\cup V^{c}$ and edges $E$,

[Expand]

equipped with orientations towards the root, orderings of incoming edges, and a partition into main and critical (leaf and root) vertices as follows:

• The edges $E\subset V\times V\setminus \Delta _{V}$ are oriented towards the root vertex $v_{0}\in V$ of the tree, so that each vertex $v\in V$ has a unique outgoing edge $e_{v}^{0}=(v,\;\cdot \;)\in E$ (except for the root vertex which has no outgoing edge) and a (possibly empty) set of incoming edges $E_{v}^{{{\rm {in}}}}=\{e=(\;\cdot \;,v)\in E\}$.
• The set of incoming edges is ordered, $E_{v}^{{{\rm {in}}}}=\{e_{v}^{1},\ldots ,e_{v}^{{|v|-1}}\}$. This induces a cyclic order on the set of all edges $E_{v}:=\{e_{v}^{0},e_{v}^{1},\ldots ,e_{v}^{{|v|-1}}\}$ adjacent to $v$, by setting $e_{v}^{{|v|}}=e_{v}^{0}$, and we will denote consecutive edges in this order by $e=e_{v}^{i},e+1=e_{v}^{{i+1}}$. In particular this yields $e_{v}^{0}+i=e_{v}^{i}$.
• The set of vertices is partitioned $V=V^{m}\sqcup V^{c}$ into the sets of main vertices $V^{m}$ and critical vertices $V^{c}=\{v_{0}^{c},v_{1}^{c},\ldots v_{d}^{c}\}$. The latter is ordered to start with the root $v_{0}^{c}=v_{0}$ and then contains d leaves $v_{i}^{c}$ of the tree, with order induced by the orientation and order of the edges.
• The root vertex $v_{0}^{c}\in V^{c}$ has a single edge $\{e_{{v_{0}}}^{1}=(v,v_{0}^{c})\}=E_{{v_{0}}}^{{{\rm {in}}}}=E_{{v_{0}}}$, and this attaches to a main vertex $v\in V^{m}$ except for one special case: For $d=1$ and $L_{d}=L_{0}$ we allow the tree with a single edge $e=(v_{1}^{c},v_{0}^{c})$ between its two critical vertices $V=\{v_{0}^{c},v_{1}^{c}\}$.

2. The tree structure induces tuples of Lagrangians $\underline {L}=(\underline {L}^{v})_{{v\in V^{m}}}$

[Expand]

that label the boundary components of domains in overall counter-clockwise order $L_{0},\ldots ,L_{d}$ as follows:

• For each main vertex $v\in V^{m}$ the Lagrangian label $\underline {L}^{v}=(L_{e}^{v})_{{e\in E_{v}}}$ is a cyclic sequence of Lagrangians $L_{e}^{v}\in \{L_{0},\ldots ,L_{d}\}$ indexed by the adjacent edges $E_{v}$ (which will become the boundary condition on $(\partial \Sigma ^{v})_{e}$).
• For each edge $e=(v^{-},v^{+})\in E$ the Lagrangian labels satisfy a matching condition as follows:
  • The edge from a critical leaf $v^{-}=v_{i}^{c}\in V^{c}$ requires $L_{e}^{{v^{+}}}=L_{i},L_{{e-1}}^{{v^{+}}}=L_{{i-1}}$.
  • The edge to the critical root $v^{+}=v_{0}^{c}\in V^{c}$ requires $L_{e}^{{v^{-}}}=L_{0},L_{{e-1}}^{{v^{-}}}=L_{d}$.
  • Any edge between main vertices $v^{-},v^{+}\in V^{m}$ requires $L_{{e}}^{{v^{-}}}=L_{{e-1}}^{{v^{+}}}$ and $L_{{e-1}}^{{v^{-}}}=L_{{e}}^{{v^{+}}}$.
  • Since $T$ has no further leaves, this determines the Lagrangian labels uniquely.

3. $\underline {\gamma }=(\underline {\gamma }_{e})_{{e\in E}}$ is a tuple of generalized Morse trajectories

[Expand]

in the following compactified Morse trajectory spaces:

• Any edge $e=(v_{i}^{c},w)$ from a critical leaf $v_{i}^{c}$ to a main vertex $w\in V^{m}$ is labeled by a half-infinite Morse trajectory $\underline {\gamma }_{e}\in \overline {\mathcal {M}}(x_{i},L_{i})$ if $L_{{i-1}}=L_{i}$, resp. by the constant $\underline {\gamma }_{e}\equiv x_{i}\in {{\rm {Crit}}}(L_{{i-1}},L_{i})$ in the discrete space $\phi _{i}(L_{{i-1}})\cap L_{i}$ if $L_{{i-1}}\neq L_{i}$.
• If the edge to the root $e=(v,v_{0}^{c})$ attaches to a main vertex $v\in V^{m}$ then it is labeled by a half-infinite Morse trajectory $\underline {\gamma }_{e}\in \overline {\mathcal {M}}(L_{0},x_{0})$ if $L_{d}=L_{0}$, resp. by the constant $\underline {\gamma }_{e}\equiv x_{0}\in {{\rm {Crit}}}(L_{d},L_{0})$ in the discrete space $\phi _{0}(L_{d})\cap L_{0}$ if $L_{d}\neq L_{0}$.
• An edge $e=(v_{i}^{c},v_{j}^{c})$ between critical vertices is labeled by an infinite Morse trajectory $\underline {\gamma }_{e}\in \overline {\mathcal {M}}(x_{i},x_{j})$ (this occurs only for $d=1$ with $L_{0}=L_{1}$ and the tree with one edge $e=(v_{1}^{c},v_{0}^{c})$).
• Any edge $e=(v,w)$ between main vertices $v,w\in V^{m}$ is labeled by a finite or infinite Morse trajectory $\underline {\gamma }_{e}\in \overline {\mathcal {M}}(L_{e}^{v},L_{e}^{v})$ in case $L_{e}^{v}=L_{{e-1}}^{v}$, resp. by a constant $\underline {\gamma }_{e}\equiv x_{e}\in {{\rm {Crit}}}(L_{{e-1}}^{v},L_{{e}}^{v})$ in the discrete space $\phi _{{L_{{e-1}}^{v},L_{{e}}^{v}}}(L_{{e-1}}^{v})\cap L_{e}^{v}$ in case $L_{e}^{v}\neq L_{{e-1}}^{w}$. (Recall the matching condition $L_{e}^{v}=L_{{e-1}}^{w}$ and $L_{{e-1}}^{v}=L_{e}^{w}$ from 2.)

4. $\underline {z}=(\underline {z}_{v})_{{v\in V^{m}}}$ is a tuple of boundary points

[Expand]

that correspond to the edges of 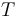$T$, are ordered counter-clockwise, and associate complex domains $\Sigma ^{v}:=D\setminus \underline {z}_{v}$ to the vertices as follows:

• For each main vertex $v$ there are $|v|$ pairwise disjoint marked points $\underline {z}_{v}=(z_{e}^{v})_{{e\in E_{v}}}\subset \partial D$ on the boundary of a disk.
• The order $E_{v}=\{e_{v}^{0},e_{v}^{1},\ldots ,e_{v}^{{|v|-1}}\}$ of the edges corresponds to a counter-clockwise order of the marked points $z_{{e_{v}^{0}}}^{v},z_{{e_{v}^{1}}}^{v},\ldots ,z_{{e_{v}^{{|v|-1}}}}^{v}\in \partial D$.
• The marked points can also be denoted as $z_{e}^{-}=z_{e}^{v}$ and $z_{e}^{+}=z_{e}^{w}$ by the edges $e=(v,w)\in E$ for which $v\in V^{m}$ or $w\in V^{m}$
• To each main vertex $v\in V^{m}$ we associate the punctured disk $\Sigma ^{v}:=D\setminus \underline {z}_{v}$. Then the marked points $\underline {z}^{v}=(z_{e}^{v})_{{e\in E_{v}}}\subset \partial D$ partition the boundary into $|v|$ connected components $\partial \Sigma ^{v}=\textstyle \sqcup _{{e\in E_{v}}}(\partial \Sigma ^{v})_{e}$ such that the closure of each component $(\partial \Sigma ^{v})_{e}$ contains the marked points $z_{e}^{v},z_{{e+1}}^{v}$.

5. $\underline {w}=(\underline {w}_{v})_{{v\in V^{m}}}$ is a tuple of sphere bubble tree attaching points for each main vertex $v\in V^{m}$, given by an unordered subset $\underline {w}_{v}\subset \Sigma ^{v}\setminus \partial \Sigma ^{v}$ of the interior of the domain.

6. $\underline {{\hat \beta }}=({\hat \beta }_{w})_{{w\in \underline {w}}}\subset \overline {\mathcal {M}}_{{0,1}}(J)$ is a tuple of not not-necessarily-pseudoholomorphic trees of sphere maps ${\hat \beta }_{w}\in \overline {\mathcal {M}}_{{0,1}}(J)$ indexed by the disjoint union $\underline {w}=\textstyle \bigsqcup _{{v\in V^{m}}}\underline {w}_{v}$ of sphere bubble tree attaching points. Each

$\beta _{w}(T^{w},\underline {z}^{w},\underline {u}^{w})$, where

a. $T^{w}$ is a tree with sets of vertices $V^{w}$ and edges $E^{w}$, and a distinguished root vertex $v_{0}^{w}\in V^{w}$, which we use to orient all edges towards the root.

b. $\underline {z}^{w}=(\underline {z}_{v}^{w})_{{v\in V^{w}}}$ is a tuple of marked points on the spherical domains $\Sigma ^{{w,v}}=S^{2}$,

[Expand]

indexed by the edges of $T^{w}$, and including a special root marked point as follows:

• For each vertex $v\neq v_{0}^{w}$ the tuple of mutually disjoint marked points $\underline {z}_{v}^{w}=(z_{e}^{{w,v}})_{{e\in E_{v}}}\subset S^{2}$ is indexed by the edges $E_{v}^{w}=\{e\in E^{w}\,|\,e=(v,\,\cdot \,)\;{\text{or}}\;e=(\,\cdot \,,v)\}$ adjacent to $v$.
• For the root vertex $v_{0}^{w}$ the tuple of mutually disjoint marked points $\underline {z}_{v}^{w}=(z_{e}^{{w,v}})_{{e\in E_{{v_{0}}}^{w}}}\subset S^{2}$ is also indexed by the edges adjacent to $v_{0}^{w}$, but is also required to be disjoint from the fixed marked point $z_{0}^{w}=0\in S^{2}\simeq \mathbb{C} \cup \{\infty \}$.
• The marked points, except for $z_{0}^{w}$, can also be denoted as $z_{e}^{{w,-}}=z_{e}^{{w,v^{-}}}$ and $z_{e}^{{w,+}}=z_{e}^{{w,v^{+}}}$ by the edges $e=(v^{-},v^{+})\in E$.

c. $\underline {u}^{w}=(\underline {u}_{v}^{w})_{{v\in V^{w}}}$ is a tuple of not-necessarily-pseudoholomorphic sphere maps' for each vertex,

[Expand]

that is each $v\in V^{w}$ is labeled by a continuous map $u_{v}^{w}:S^{2}\to M$ satisfying $Sobolevregularity$ and matching conditions as follows:

• TODO: $H^{{3,\delta }}$-Sobolev regularity ... on punctured spheres ?!?
• The matching conditions are $u_{{v^{-}}}^{w}(z_{e}^{{w,-}})=u_{{v^{+}}}^{w}(z_{e}^{{w,+}})$ for each edge $e=(v^{-},v^{+})\in E$.

7. $\underline {u}=(\underline {u}_{v})_{{v\in V^{m}}}$ is a tuple of not-necessarily-pseudoholomorphic disk maps for each main vertex,

[Expand]

that is each $v\in V^{m}$ is labeled by a continuous map $u_{v}:\Sigma ^{v}\to M$ satisfying a Sobolev regularity, Lagrangian boundary conditions, and matching conditions as follows:

• TODO: $H^{{3,\delta }}$-Sobolev regularity - and make sure it implies uniform convergence
• The Lagrangian boundary conditions are $u_{v}(\partial \Sigma ^{v})\subset \underline {L}^{v}$; more precisely this requires $u_{v}{\bigl (}(\partial \Sigma ^{v})_{e}{\bigr )}\subset L_{e}^{v}$ for each adjacent edge $e\in E_{v}$.
• The finite energy condition is $\textstyle \int _{{\Sigma ^{v}}}u_{v}^{*}\omega <\infty$.
• The matching conditions for sphere bubble trees are $u^{v}(w)={\text{ev}}_{0}(\beta _{w})$ for each main vertex $v\in V^{m}$ and sphere bubble tree attaching point $w\in \underline {w}_{v}$.
• The Sobolev regularity implies uniform convergence of $u_{v}$ near each puncture $z_{e}^{v}$, and the limits are required to satisfy the following matching conditions:
  • For edges $e\in E_{v}$ whose Lagrangian boundary conditions $L_{{e-1}}^{v}=L_{e}^{v}$ agree, the map $u_{v}$ extends smoothly to the puncture $z_{e}^{v}$, and its value is required to match with the evaluation of the Morse trajectory $\underline {\gamma }_{e}$ associated to the edge $e=(v_{e}^{-},v_{e}^{+})$, that is $u_{v}(z_{e}^{v})={{\rm {ev}}}^{\pm }(\underline {\gamma }_{e})$ for $v=v_{e}^{\mp }$.
  • For edges $e\in E_{v}$ with different Lagrangian boundary conditions $L_{{e-1}}^{v}\neq L_{e}^{v}$, the map $u_{e}^{v}:=(\iota _{e}^{v})^{*}u_{v}:(-\infty ,0)\times [0,1]\to M$ has a uniform limit $\lim _{{s\to -\infty }}u^{v}(s,t)=\phi _{{L_{{e-1}}^{v},L_{e}^{v}}}^{{t-1}}(x_{e})$ for some $x_{e}\in \phi _{{L_{{e-1}}^{v},L_{e}^{v}}}(L_{{e-1}}^{v})\cap L_{e}^{v}={\text{Crit}}(L_{{e-1}}^{v},L_{e}^{v})$, and this limit intersection point is required to match with the value of the constant 'Morse trajectory' $\underline {\gamma }_{e}\in {\text{Crit}}(L_{{e-1}}^{v},L_{e}^{v})$ associated to the edge $e=(v_{e}^{-},v_{e}^{+})$, that is $x_{e}=\lim _{{s\to -\infty }}u^{v}(s,1)=\underline {\gamma }_{e}$.

8. The generalized pseudoholomorphic polygon is stable

[Expand]

in the following sense: TODO: update to Ham pert, sphere bubble tree

• Any main vertex $v\in V^{m}$ whose map has zero energy $\textstyle \int u_{v}^{*}\omega =0$ has enough special points to have trivial isotropy, that is the number of boundary marked points $|v|=\#\underline {z}_{v}$ plus twice the number of interior marked points $\#\underline {w}_{v}$ is at least 3.
• The sphere bubble tree is stable

[Expand]

in the sense that

any vertex $v\in V$ whose map has zero energy $\textstyle \int u_{v}^{*}\omega =0$ (which is equivalent to $u_{v}$ being constant) has valence $|v|\geq 3$. Here the marked point $z_{0}$ counts as one towards the valence $|v_{0}|$ of the root vertex; in other words the root vertex can be constant with just two adjacent edges.

Finally, two generalized pseudoholomorphic polygons are equivalent $(T,\underline {\gamma },\underline {z},\underline {w},\underline {\beta },\underline {u})\sim (T',\underline {\gamma }',\underline {z}',\underline {w}',\underline {\beta }',\underline {u}')$ if

[Expand]

there is a tree isomorphism $\zeta :T\to T'$ and a tuple of disk biholomorphisms $(\psi _{v}:D\to D)_{{v\in V^{m}}}$ which preserve the tree, Morse trajectories, marked points, and maps in the sense that

• $\zeta$ preserves the tree structure and order of edges;
• $\underline {\gamma }_{e}=\underline {\gamma }'_{{\zeta (e)}}$ for every $e\in E$;
• $\psi _{v}(z_{e}^{v})={z'}_{{\zeta (e)}}^{{\zeta (v)}}$ for every $v\in V^{m}$ and adjacent edge $e\in E_{v}$;
• $\psi _{v}(\underline {w}_{v})=\underline {w}'_{{\zeta (v)}}$ for every $v\in V^{m}$;
• $\beta _{w}=\beta '_{{\psi _{v}(w)}}$ for every $v\in V^{m}$ and $w\in \underline {w}_{v}$;
• the maps are related by reparametrization, $u_{v}=u'_{{\zeta (v)}}\circ \psi _{v}$ for every $v\in V^{m}$.

---

The symplectic area function

If no Hamiltonian perturbations are involved in the construction of a moduli space of generalized pseudoholomorphic polygons - i.e. if for each pair $\{i,j\}\subset \{0,\ldots ,d\}$ the Lagrangians are either identical $L_{i}=L_{j}$ or transverse $L_{i}\pitchfork L_{j}$ - then the symplectic area function on the moduli space is defined by

$\omega :\overline {\mathcal {M}}(x_{0};x_{1},\ldots ,x_{d})\to \mathbb{R} ,\quad b={\bigl [}T,\underline {\gamma },\underline {z},\underline {w},\underline {\beta },\underline {u}{\bigr ]}\mapsto \omega (b):=\sum _{{v\in V^{m}}}\textstyle \int _{{\Sigma _{v}}}u_{v}^{*}\omega \;+\;\sum _{{\beta _{w}\in \underline {\beta }}}\omega (\beta _{w})=\langle [\omega ],[b]\rangle ,$

which - since $\omega |_{{L_{i}}}\equiv 0$ only depends on the total homology class of the generalized polygon

$[b]:=\sum _{{v\in V}}(\overline {u}_{v})_{*}[D]+\sum _{{\beta _{w}\in \underline {\beta }}}[\beta _{w}]\;\in \;H_{2}(M;L_{0}\cup L_{1}\ldots \cup L_{d}).$

Here $\overline {u}_{v}:D\to M$ is defined by unique continuous continuation to the punctures $z_{e}^{v}$ at which $L_{{e-1}}^{v}=L_{e}^{v}$ or $L_{{e-1}}^{v}\pitchfork L_{e}^{v}$.

[Expand]

Differential Geometric TODO:

In the presence of Hamiltonian perturbations, the definition of the symplectic area function needs to be adjusted to match with the symplectic action functional on the Floer complexes and satisfy some properties (which also need to be proven in the unperturbed case):

• $\omega (b)$ is invariant under deformations with fixed limits (used in proof of A-infty relations and invariance);
• a bound on $\omega (b)$ needs to imply Gromov-compactness ... which requires an area-energy identity for J-curves, but we are allowed (bounded!) error terms from e.g. Hamiltonian perturbations;
• invariance proofs arguing with 'upper triangular form' require contributions to $\mu ^{1}$ to be of positive symplectic area, or constant strips/disks for zero symplectic area;
• to work with the Novikov ring, rather than field, the symplectic area needs to be nonnegative for all polygons (not just the strips and other contributions to $\mu ^{1}$ for which this is automatic). It *might* be possible to achieve this by remembering that the Hamilton functions for each pair of Lagrangians are only fixed up to a constant (not see in the Hamiltonian vector field or time-1-flow), so when constructing the Hamiltonian perturbation vector fields over Deligne-Mumford spaces, it might be possible to shift e.g. the outgoing Hamiltonian in such a way that the vector field can be constructed with 'curvature terms of the correct sign'.

Sphere bubble trees

Finally, two sphere bubble trees are equivalent $(T,\underline {z},\underline {u})\sim (T',\underline {z}',\underline {u}')$ if

[Expand]

there is a tree isomorphism $\zeta :T\to T'$ and a tuple of sphere biholomorphisms $(\psi _{v}:S^{2}\to S^{2})_{{v\in V}}$ which preserve the tree, marked points, and pseudoholomorphic curves in the sense that

• $\zeta$ preserves the tree structure, in particular maps the root $v_{0}$ to the root $v_{0}'$;
• $\psi _{{v_{0}}}(0)=0$ and $\psi _{v}(z_{e}^{v})={z'}_{{\zeta (e)}}^{{\zeta (v)}}$ for every $v\in V$ and adjacent edge $e\in E_{v}$;
• the pseudoholomorphic spheres are related by reparametrization, $u_{v}=u'_{{\zeta (v)}}\circ \psi _{v}$ for every $v\in V$.

---

[Expand]