Polyfold constructions for Fukaya categories
From Polyfolds.org
Revision as of 20:09, 19 May 2017 by KatrinWehrheim (Talk | contribs)
Fukaya categories capture the chain level information contained in Lagrangian Floer theory and its product structures.
There are different constructions (and even more proposals) depending on the properties of the (fixed) ambient symplectic manifold.
For example, Seidel [1] considers exact symplectic manifolds and constructs an (uncurved) Fukaya 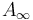 category whose objects are exact Lagrangians (with a ``brane structure), whose morphism spaces are Floer complexes (depending on the choice of a Hamiltonian) by counting pseudoholomorphic polygons with boundary on the Lagrangians.
category whose objects are exact Lagrangians (with a ``brane structure), whose morphism spaces are Floer complexes (depending on the choice of a Hamiltonian) by counting pseudoholomorphic polygons with boundary on the Lagrangians.
(which are necessarily noncompact but assumed to satisfy certain boundedness conditions)
For now we will restrict ourselves to the
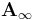 Relations
Relations