Polyfold constructions for Fukaya categories
Fukaya categories capture the chain level information contained in Lagrangian Floer theory and its product structures. For an introduction see e.g. Auroux' Beginner's introduction to Fukaya categories [1].
There are different constructions (and even more proposals) depending on the properties of the (fixed) ambient symplectic manifold.
For example, Seidel [2] considers exact symplectic manifolds and constructs an (uncurved) Fukaya 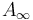 category whose objects are exact Lagrangians (with a brane structure), whose morphism spaces are Floer complexes (depending on the choice of a Hamiltonian), and whose composition operations are given by counting pseudoholomorphic polygons with boundary on the Lagrangians.
(Here the benefit of the exactness assumption is that bubbling is excluded, so that the moduli spaces can be regularized by geometric methods (choices of Hamiltonian perturbations and almost complex structures). On the other hand, exact symplectic manifolds (on which the symplectic 2-form is exact) are necessarily noncompact, so one needs to assume certain boundedness and convexity conditions to ensure that pseudoholomorphic curves do not escape to infinity.)
category whose objects are exact Lagrangians (with a brane structure), whose morphism spaces are Floer complexes (depending on the choice of a Hamiltonian), and whose composition operations are given by counting pseudoholomorphic polygons with boundary on the Lagrangians.
(Here the benefit of the exactness assumption is that bubbling is excluded, so that the moduli spaces can be regularized by geometric methods (choices of Hamiltonian perturbations and almost complex structures). On the other hand, exact symplectic manifolds (on which the symplectic 2-form is exact) are necessarily noncompact, so one needs to assume certain boundedness and convexity conditions to ensure that pseudoholomorphic curves do not escape to infinity.)
This wiki will focus on the main difficulty that is not addressed in Seidel's book: How to regularize the moduli spaces of pseudoholomorphic polygons when geometric methods fail (e.g. due to sphere bubbling), and how to capture disk bubbling algebraically.
To limit the classical analytic challenges in studying the pseudoholomorphic curves involved, we restrict our constructions to a fixed compact symplectic manifold 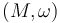 .
Then the Fukaya category of M consists of the following data:
.
Then the Fukaya category of M consists of the following data:
Objects
The Objects of 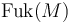 are - roughly speaking - the compact Lagrangian submanifolds
are - roughly speaking - the compact Lagrangian submanifolds 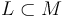 . More precisely, each object is a Lagrangian equipped with a brane structure which will induce orientations of moduli spaces and is needed to discuss the coefficient systems for the Floer theory.
. More precisely, each object is a Lagrangian equipped with a brane structure which will induce orientations of moduli spaces and is needed to discuss the coefficient systems for the Floer theory.
Here input from the Mirror Symmetry community is needed to determine what specific brane structures and coefficient systems should be used. For the time being, we will treat brane structures as abstract gadget that induces orientations on the moduli spaces and denote the coefficient system (often a field) by 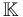 .
.
Morphisms
For two Lagrangians 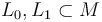 that are transverse (i.e.
that are transverse (i.e. 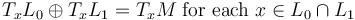 ) and hence have a finite set of intersection points, the natural choice of morphism space is
) and hence have a finite set of intersection points, the natural choice of morphism space is
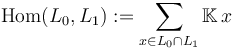 .
.
When 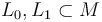 are not transverse, then we will choose a Hamiltonian symplectomorphism
are not transverse, then we will choose a Hamiltonian symplectomorphism 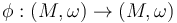 such that
such that 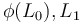 are transverse, and define
are transverse, and define 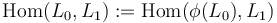 .
.
When considering the isomorphism space 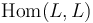 of a fixed Lagrangian
of a fixed Lagrangian 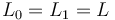 , then the Hamiltonian symplectomorphism
, then the Hamiltonian symplectomorphism 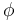 can be obtained by lifting a Morse function
can be obtained by lifting a Morse function 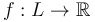 to a Hamiltonian function in a neighborhood
to a Hamiltonian function in a neighborhood 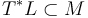 . After extending it suitably, the intersection points can be identified with the critical points,
. After extending it suitably, the intersection points can be identified with the critical points, 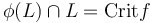 . Thus in this case we define
. Thus in this case we define
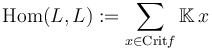 .
.Each of the sets of homomorphisms defined above is a vector space over the field 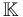 .
For most versions of Fukaya categories, these vector spaces should also be graded over
.
For most versions of Fukaya categories, these vector spaces should also be graded over 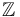 or
or 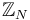 . This grading will arise from additional data in the brane structure for each Lagrangian.
. This grading will arise from additional data in the brane structure for each Lagrangian.
Here the choice of the Morse complex for the isomorphism spaces is based on input from the Mirror Symmetry community. Further input is needed to decide how to track or deal with these choices algebraically, and which exact gradings to use - depending on the desired brane structures.
Composition Operations
While a category has a single composition map 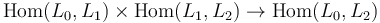 , an
, an 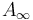 -category has composition maps of every order
-category has composition maps of every order 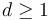 ,
,
 -Relations
-Relations