Polyfold constructions for Fukaya categories
Fukaya categories were first introduced by Fukaya, Oh, Ohta, Ono in ca.2000. They capture the chain level information contained in Lagrangian Floer theory and its product structures. For an introduction see e.g. Auroux' Beginner's introduction to Fukaya categories [A].
There are different constructions (and even more proposals) depending on the properties of the (fixed) ambient symplectic manifold.
This wiki will focus on the main difficulty that is not addressed in Seidel's book: How to regularize the moduli spaces of pseudoholomorphic polygons when geometric methods fail (e.g. due to sphere bubbling), and how to capture disk bubbling algebraically.
To limit the classical analytic challenges in studying the pseudoholomorphic curves involved, we restrict our constructions to a fixed compact symplectic manifold 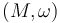 .
Then - depending on various open choices and algebraic packaging for which we seek input from the Mirror Symmetry community - the Fukaya category
.
Then - depending on various open choices and algebraic packaging for which we seek input from the Mirror Symmetry community - the Fukaya category  consists of the following data:
consists of the following data:
Objects
An object  of
of 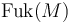 is a compact Lagrangian submanifold
is a compact Lagrangian submanifold 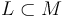 equipped with a brane structure.
equipped with a brane structure.
Here input from the Mirror Symmetry community is needed
For special symplectic manifolds (those equipped with an almost complex structure J for which all J-holomorphic spheres are constant) we could work with Lagrangians without additional brane structure. In this case of trivial brane structures we will not have gradings or orientations, and thus will have to (and can) work with 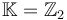 coefficients in the following.
coefficients in the following.
Morphisms
The morphism spaces of an 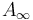 -category form graded modules over a ring.
For Fukaya categories this typically is the Novikov ring over a fixed field
-category form graded modules over a ring.
For Fukaya categories this typically is the Novikov ring over a fixed field 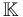 such as
such as
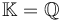 or
or 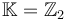 , with a variable
, with a variable 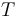 ,
,

The natural construction of the morphism spaces  arises from the geometry of the Lagrangian intersection
arises from the geometry of the Lagrangian intersection  as follows:
as follows:
The universal construction of the morphism spaces is

as module over the Novikov ring  that is freely generated by a finite critical set
that is freely generated by a finite critical set

This requires the choice of a Hamiltonian diffeomorphism  or Morse function
or Morse function  , respectively, for each pair of objects.
, respectively, for each pair of objects.
For most versions of Fukaya categories, these modules also carry a grading induced by brane structures  (or
(or  with even
with even  ) for all
) for all  .
(When working with trivial brane structures, we set
.
(When working with trivial brane structures, we set  .)
.)
Here input from the Mirror Symmetry community is needed
Composition Operations
While a category has a single composition map 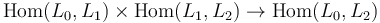 , an
, an 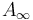 -category has composition maps of every order
-category has composition maps of every order 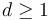 , which are
, which are  -linear maps from a tensor product of morphism spaces,
-linear maps from a tensor product of morphism spaces,

When the morphism spaces carry a grading induced by brane structures, then the composition operation  has degree
has degree  (i.e. shifts the grading down by this amount).
In particular, the
(i.e. shifts the grading down by this amount).
In particular, the  composition map
composition map  is a differential (of degree 1) on the morphism space - namely the Floer differential in the case of the Fukaya category.
For Fukaya categories of non-exact symplectic manifolds, disk bubbling will moreover result in curvature terms in the
is a differential (of degree 1) on the morphism space - namely the Floer differential in the case of the Fukaya category.
For Fukaya categories of non-exact symplectic manifolds, disk bubbling will moreover result in curvature terms in the 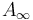 -relations, which are encoded in terms of a
-relations, which are encoded in terms of a  composition for each Lagrangian brane,
composition for each Lagrangian brane,

By linearity it suffices to construct these composition maps for any pure tensor given by intersection points  .
These constructions will result from appropriate ways of counting elements of moduli spaces of pseudoholomorphic polygons
.
These constructions will result from appropriate ways of counting elements of moduli spaces of pseudoholomorphic polygons  ,
,

Here  denotes a regularization of the moduli space (e.g. a perturbation), which in particular induces a weight function
denotes a regularization of the moduli space (e.g. a perturbation), which in particular induces a weight function  (e.g.
(e.g.  in case
in case  ),
and
),
and  is a symplectic area function.
Finally, the superscript in
is a symplectic area function.
Finally, the superscript in  indicates the part of the moduli space of expected dimension 0.
indicates the part of the moduli space of expected dimension 0.
An example of this regularization construction by means of polyfold theory can be found in [J.Li thesis], which constructs a curved 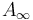 -algebra
-algebra  on the Morse complex
on the Morse complex  of a fixed Lagrangian
of a fixed Lagrangian  .
.
Curved 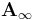 -Relations
-Relations
The 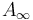 -relations generalize the associativity relation for classical composition of morphisms in categories. They also describe the failure of the Floer differential to square to zero, due to a curvature term. So, more precisely, we need to establish the curved
-relations generalize the associativity relation for classical composition of morphisms in categories. They also describe the failure of the Floer differential to square to zero, due to a curvature term. So, more precisely, we need to establish the curved 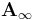 -relations.
-relations.
The curved 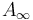 -relations can be phrased as
-relations can be phrased as  , where
, where  is given by the composition maps
is given by the composition maps  acting on the total complex
acting on the total complex
Using linearity it suffices to prove the 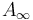 -relations for
-relations for 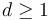 and
and 

where  .
.
To prove these identities we will identify the summands with Cartesian products of 0-dimensional parts of regularized moduli spaces, identify these with the boundary facets of 1-dimensional regularized moduli space,

where we abbreviate
 and appeal to the fact that the boundary of a sufficiently regular moduli space is null homologous.
In addition, the proof relies on additivity of the symplectic area
and appeal to the fact that the boundary of a sufficiently regular moduli space is null homologous.
In addition, the proof relies on additivity of the symplectic area  and requires the regularizations of these moduli spaces to be related by
and requires the regularizations of these moduli spaces to be related by  .
.
Invariance
There are many choices involved in the above construction of a Fukaya category. These can roughly be separated into geometric, local choices (the almost complex structure  , and Hamiltonian diffeomorphisms
, and Hamiltonian diffeomorphisms 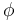 resp. Morse functions
resp. Morse functions  ) and abstract, global choices (the perturbation
) and abstract, global choices (the perturbation  and setups of ambient space/bundle in which it gets constructed). Sometimes we can even obtain the required regularization by a geometric choice of the perturbations.
and setups of ambient space/bundle in which it gets constructed). Sometimes we can even obtain the required regularization by a geometric choice of the perturbations.
To prove independence of the Fukaya category (up to an appropriate notion of equivalence) from a geometric/local choice, we can construct continuation maps
For abstract/global choices, such a continuation map PDE is not available
A general invariance proof will likely require a setup along the following lines:
To compare the Fukaya categories  resulting from two different sets of choices, use a homotopy between the perturbation data to construct an
resulting from two different sets of choices, use a homotopy between the perturbation data to construct an 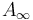 -category
-category ![{{\rm {Fuk}}}_{{[0,1]}}](/images/math/0/8/f/08f77cc8417886da549c7c998e5a369e.png) together with two restriction functors
together with two restriction functors ![{{\rm {Fuk}}}_{{[0,1]}}\to {{\rm {Fuk}}}_{0}](/images/math/7/c/2/7c27c98cea73aaf5f04ddced8b4ce71d.png) and
and ![{{\rm {Fuk}}}_{{[0,1]}}\to {{\rm {Fuk}}}_{1}](/images/math/1/7/0/17029600f3933ad6c9c3da2aee1556d9.png) .
.
Here input from the Mirror Symmetry community is needed
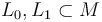 that are transverse (i.e.
that are transverse (i.e. 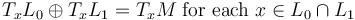 ) and hence have a finite set of intersection points, the natural choice of morphism space is the
) and hence have a finite set of intersection points, the natural choice of morphism space is the  .
.
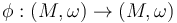 such that
such that 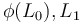 are transverse. So we define the Floer complex resp. Fukaya category morphism space by
are transverse. So we define the Floer complex resp. Fukaya category morphism space by 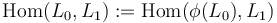 .
.
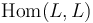 of a fixed Lagrangian
of a fixed Lagrangian 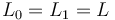 , then the Hamiltonian symplectomorphism
, then the Hamiltonian symplectomorphism 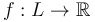 to a Hamiltonian function in a Lagrangian neighborhood
to a Hamiltonian function in a Lagrangian neighborhood 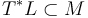 . After extending it suitably, the intersection points can be identified with the critical points,
. After extending it suitably, the intersection points can be identified with the critical points, 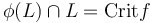 . Thus in this case we define the morphism space by the Morse chain complex
. Thus in this case we define the morphism space by the Morse chain complex
 .
. we will prescribe the canonical choice of
we will prescribe the canonical choice of  .
For each nontransverse pair
.
For each nontransverse pair  we fix an autonomous Hamiltonian function
we fix an autonomous Hamiltonian function  such that the time-1 flow
such that the time-1 flow
 of the associated Hamiltonian vector field
of the associated Hamiltonian vector field  yields the desired transversality
yields the desired transversality  .
Moreover, we can make these choices symmetric by setting
.
Moreover, we can make these choices symmetric by setting  so that
so that  . This identifies the morphism spaces
. This identifies the morphism spaces  via the bijection of critical sets
via the bijection of critical sets

 contains no
contains no  . Generalizing this work to all compact symplectic manifolds requires inclusion of sphere bubble trees, which cause nontrivial isotropy. In that case, the need for multivalued perturbations rules out working with
. Generalizing this work to all compact symplectic manifolds requires inclusion of sphere bubble trees, which cause nontrivial isotropy. In that case, the need for multivalued perturbations rules out working with 
 by
by  .
Now the abstract sum of all composition maps
.
Now the abstract sum of all composition maps  is a
is a  that is given on pure tensors by
that is given on pure tensors by

 into pure tensors of lengths
into pure tensors of lengths  , in particular allow
, in particular allow  to have length
to have length  .
The sign
.
The sign  is determined by the length \ell(c_n \otimes \ldots \otimes c_1) = n) and the
is determined by the length \ell(c_n \otimes \ldots \otimes c_1) = n) and the  (or
(or  with even
with even 


 consists of pairs
consists of pairs
 for any
for any  and
and  .
Since the symplectic area is constant on every connected component of the moduli space, we can partition the claimed identity into sums of the weight function over the boundary of a union of components,
.
Since the symplectic area is constant on every connected component of the moduli space, we can partition the claimed identity into sums of the weight function over the boundary of a union of components,
 for some
for some  .
Now the
.
Now the 
 are generally not given by a local differential operator - i.e.
are generally not given by a local differential operator - i.e.  depends on the entire map
depends on the entire map  , not just on the value
, not just on the value  and some derivatives of
and some derivatives of  at the point
at the point  . Instead, one is led to considering a 1-parameter family of Cauchy-Riemann PDEs which interpolates between the two abstract choices. This homotopy method was originally introduced by Floer, and is outlined in the exact
. Instead, one is led to considering a 1-parameter family of Cauchy-Riemann PDEs which interpolates between the two abstract choices. This homotopy method was originally introduced by Floer, and is outlined in the exact