Difference between revisions of "Regularized moduli spaces"

From Polyfolds.org
Jump to: navigation, search
(→‎Abstract, Coherent Regularization)
(→‎Abstract, Coherent Regularization)
Line 13: Line 13:
 
</math>
 
</math>
 
</center>
 
</center>
−
In order to obtain boundary stratifications which imply the <math>A_\infty</math>-relations, any abstract approach needs to regularize "coherently’’ (whereas geometric regularizations are automatically coherent), that is compatible with the boundary stratification of the ambient spaces <math>\mathcal{X}(\underline{x})</math> being given by fiber products of other ambient spaces. In our setup, these fiber products are over finite sets of Morse and Floer critical points, so simplify to unions of Cartesian products,  
+
In order to obtain boundary stratifications which imply the <math>A_\infty</math>-relations, any abstract approach needs to regularize "coherently" (whereas geometric regularizations are automatically coherent), that is compatible with the boundary stratification of the ambient spaces <math>\mathcal{X}(\underline{x})</math> being given by fiber products of other ambient spaces. In our setup, these fiber products are over finite sets of Morse and Floer critical points, so simplify to unions of Cartesian products,  
 
<center>
 
<center>
 
<math>
 
<math>

Revision as of 13:11, 3 June 2017

table of contents

Abstract, Coherent Regularization

In order to regularize the moduli spaces of pseudoholomorphic polygons \overline {\mathcal {M}}(x_{0};x_{1},\ldots ,x_{d}) for each tuple of Lagrangians \underline {L}={\bigl (}L_{0},\ldots ,L_{d}\subset M{\bigr )}, generators \underline {x}={\bigl (}x_{0}\in {\text{Crit}}(L_{0},L_{d}),x_{1}\in {\text{Crit}}(L_{0},L_{1}),\ldots ,x_{d}\in {\text{Crit}}(L_{{d-1}},L_{d}){\bigr )}, and a fixed compatible almost complex structure J, any abstract regularization approach (opposed to geometric ones, as contrasted in [section 3, FFGW] and [sections 2.1-2, MW]) starts by describing each Gromov-compactified moduli space as

{\text{zero set}}\quad \overline {\mathcal {M}}(\underline {x})=\overline \partial _{{J,Y}}^{{-1}}(0)\quad {\text{of a section}}\quad \overline \partial _{{J,Y}}:{\mathcal {X}}(\underline {x})\to {\mathcal {Y}}_{J}(\underline {x})\quad {\text{of a bundle}}\quad \pi :{\mathcal {Y}}_{J}(\underline {x})\to {\mathcal {X}}(\underline {x}).

In order to obtain boundary stratifications which imply the 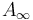A_{\infty }-relations, any abstract approach needs to regularize "coherently" (whereas geometric regularizations are automatically coherent), that is compatible with the boundary stratification of the ambient spaces {\mathcal {X}}(\underline {x}) being given by fiber products of other ambient spaces. In our setup, these fiber products are over finite sets of Morse and Floer critical points, so simplify to unions of Cartesian products,

\partial {\mathcal {X}}(x_{0};x_{1},\ldots ,x_{d})=\bigsqcup _{{m,n\geq 0}}\bigsqcup _{{y\in {\text{Crit}}(L_{n},L_{{m+n}})}}{\mathcal {X}}(y;x_{{n+1}}\ldots x_{{n+m}})\times {\mathcal {X}}(x_{0};x_{1}\ldots x_{n},y,x_{{n+m+1}}\ldots x_{d}).

[Expand]

In the abstract regularization approach of [2015-FOOO1], [2017-FOOO2], and most other virtual approaches, the global sections s:{\mathcal {X}}\to {\mathcal {Y}} are patched together from smooth sections of finite rank bundles over finite dimensional manifolds s_{i}:X_{i}\to Y_{i}. While at first glance this resolves most analytic issues (up to the question of obtaining smooth sections near nodal curves from the classical gluing analysis), it introduces a number of subtle combinatorial, algebraic, and topological challenges as discussed in [MW].

In the abstract regularization approach via polyfold theory [HWZ], the ambient space {\mathcal {X}} is chosen ‘large enough’ to be fairly natural, allow for restrictions and fiber products, and so that the section \overline \partial _{{J,Y}} is directly given by a Cauchy-Riemann operator. While this resolves most combinatorial, algebraic, and topological challenges - by building a natural ambient space that is e.g. Hausdorff and provides natural compactness controls - equipping this ambient space with a notion of smooth structure posed analytic issues that were insurmountable with classical infinite dimensional analysis.

Polyfold Fredholm Descriptions of Moduli spaces

To overcome the analytic challenges, the abstract parts of polyfold theory provide alternative notions of infinite dimensional spaces and differentiability with which we will be able to

  • equip each ambient space {\mathcal {X}}(\underline {x}) with a smooth structure as 'polyfold modeled on sc-Hilbert spaces';
  • equip each ambient bundle \pi :{\mathcal {Y}}_{J}(\underline {x})\to {\mathcal {X}}(\underline {x}) with a smooth bundle structure as 'strong polyfold bundle over {\mathcal {X}}(\underline {x})';
  • show that each Cauchy-Riemann section \overline \partial _{{J,Y}}:{\mathcal {X}}(\underline {x})\to {\mathcal {Y}}_{J}(\underline {x}) satisfies adapted notions of smoothness and nonlinear Fredholm properties, i.e. is a 'sc-Fredholm section of the polyfold bundle \pi :{\mathcal {Y}}_{J}(\underline {x})\to {\mathcal {X}}(\underline {x})'.

Before we can use the abstract perturbation results from polyfold theory to regularize the zero sets \overline \partial _{{J,Y}}^{{-1}}(0)\subset {\mathcal {X}}(\underline {x}), we need to restrict ourselves to (unions of) connected components of the ambient space within which the zero set is compact. Moreover, we will ultimately just need the zero sets of specific Fredholm indices. So for any k\in \mathbb{Z } ,w_{0}\in \mathbb{R} we define

\overline {\mathcal {M}}^{k}(\underline {x}):={\bigl \{}b\in \overline {\mathcal {M}}(\underline {x})\,{\big |}\,{\text{ind}}\,{{\rm {D}}}_{b}\overline \partial _{{J,Y}}=k{\bigr \}},\qquad \overline {\mathcal {M}}_{{w_{0}}}(\underline {x}):={\bigl \{}b\in \overline {\mathcal {M}}(\underline {x})\,{\big |}\,\omega (b)\leq w_{0}{\bigr \}}.

Here the linearized section {{\rm {D}}}_{b}\overline \partial _{{J,Y}} has a well defined Fredholm index in \mathbb{Z } at any solution b\in \overline \partial _{{J,Y}}^{{-1}}(0), and \omega is the symplectic area function defined on Moduli spaces of pseudoholomorphic polygons. We will extend both to locally constant functions on the ambient spaces, {{\rm {ind}}}:{\mathcal {X}}(\underline {x})\to \mathbb{Z } and \omega :{\mathcal {X}}(\underline {x})\to \mathbb{R} , and thus obtain ambient spaces for \overline {\mathcal {M}}^{k}(\underline {x}) and \overline {\mathcal {M}}_{{w_{0}}}(\underline {x}),

{\mathcal {X}}^{k}(\underline {x}):={\bigl \{}b\in {\mathcal {X}}(\underline {x})\,{\big |}\,{\text{ind}}(b)=k{\bigr \}},\qquad {\mathcal {X}}_{{w_{0}}}(\underline {x}):={\bigl \{}b\in {\mathcal {X}}(\underline {x})\,{\big |}\,\omega (b)\leq w_{0}{\bigr \}}.

[Expand]

Now Gromov compactness can be formulated as saying that for any w_{0}\in \mathbb{R} the restricted section \overline \partial _{{J,Y}}|_{{{\mathcal {X}}_{{w_{0}}}(\underline {x})}}:{\mathcal {X}}_{{w_{0}}}(\underline {x})\to {\mathcal {Y}}_{J}(\underline {x})|_{{{\mathcal {X}}_{{w_{0}}}(\underline {x})}}:=\pi ^{{-1}}{\bigl (}{\mathcal {X}}_{{w_{0}}}(\underline {x}){\bigr )} is a proper Fredholm section (of a strong polyfold bundle over a polyfold that is modeled on sc-Hilbert spaces).

Polyfold Regularizations

In the special case of trivial isotropy - when each {\mathcal {X}}_{{w_{0}}}(\underline {x}) is an M-polyfold - the abstract M-polyfold perturbation and implicit function theorem package [Theorem 5.18 HWZ] then provides, for any w_{0}\in \mathbb{R} , a perturbation s_{{w_{0}}}:{\mathcal {X}}_{{w_{0}}}(\underline {x})\to {\mathcal {Y}}_{J}(\underline {x})|_{{{\mathcal {X}}_{{w_{0}}}(\underline {x})}} that is transverse to \overline \partial _{{J,Y}} and controls compactness such that the perturbed solution set {\bigl \{}b\in {\mathcal {X}}_{{w_{0}}}(\underline {x})\,{\big |}\,\overline \partial _{{J,Y}}(b)=s_{{w_{0}}}(b){\bigr \}} inherits the structure of a compact manifold with boundary and corners induced by intersections with the boundary and corner structures of {\mathcal {X}}_{{w_{0}}}(\underline {x}). We will see below that this perturbation section s_{{w_{0}}} can in fact be extended to all of {\mathcal {X}}(\underline {x}). However, in the case of nontrivial isotropy, we will have to work with multi-sections \tau :{\mathcal {Y}}_{J}(\underline {x})\to \mathbb{Q} ^{+}. These are related to sections in the case of trivial isotropy by a section s:{\mathcal {X}}(\underline {x})\to {\mathcal {Y}}_{J}(\underline {x}) inducing a multi-section given by \tau (\eta )=1 iff \eta =s(\pi (b)), and \tau _{{w_{0}}}(\eta )=0 otherwise.

[Expand]

In the general case of nontrivial isotropy, we moreover require orientations of Cauchy-Riemann sections before we can construct a multi-valued perturbation \nu :{\mathcal {Y}}_{J}(\underline {x})\to \mathbb{Q} ^{+} such that the perturbed solution set

\overline {\mathcal {M}}(\underline {x};\nu ):={\bigl \{}b\in {\mathcal {X}}(\underline {x})\,{\big |}\,\nu {\bigl (}\overline \partial _{{J,Y}}(b){\bigr )}>0{\bigr \}}

is a branched suborbifold of the polyfold {\mathcal {X}}_{{w_{0}}}(\underline {x}) such that \overline {\mathcal {M}}(\underline {x};\nu )\cap {\mathcal {X}}_{{w_{0}}}(\underline {x}) is compact for any w_{0}\in \mathbb{R} . (Moreover, this branched orbifold is weighted by the restriction \nu |_{{\overline {\mathcal {M}}(\underline {x};\nu )}}:\overline {\mathcal {M}}(\underline {x};\nu )\to \mathbb{Q} .)

Construction of Composition Operations

For the Composition Operators in the Polyfold Constructions for Fukaya Categories to be well defined we need to check that \textstyle \sum _{{b\in \overline {\mathcal {M}}^{0}(\underline {x})}}\nu (b)\,T^{{\omega (b)}} defines an element in the Novikov ring. This requires the following two properties of the perturbed solution sets:

[Expand]

Every perturbed solution b\in \overline {\mathcal {M}}^{0}(x_{0};x_{1},\ldots ,x_{d};\nu ) needs to have nonnegative symplectic area \omega (b)\geq 0. This is achieved as follows:

[Expand]

Here input from the Mirror Symmetry community is needed

[Expand]Any subset of perturbed solutions

\overline {\mathcal {M}}^{0}(\underline {x};\nu )\cap {\mathcal {X}}_{{w_{0}}}(\underline {x}) of Fredholm index {{\rm {ind}}}\,D_{b}\overline \partial _{{J,Y}}=0 and bounded energy \omega (b)\leq w_{0} for some w_{0}>0 needs to be a finite set. This is true by the following:


WORK IN PROGRESS

CAUTION: need to divide by order of isotropy to get weight functions ?!?

Proof of 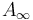A_{\infty }-relations



[Expand]



we need to explain how to obtain regularizations \overline {\mathcal {M}}^{k}(x_{0};x_{1},\ldots ,x_{d};\nu ) for expected dimensions k=0,1 by a choice of perturbations \nu . Moreover, we need to choose these perturbations coherently to ensure that the boundary of each 1-dimensional part is given by Cartesian products of 0-dimensional parts,

\partial \overline {\mathcal {M}}^{1}(x_{0};x_{1},\ldots ,x_{d};\nu )=\bigsqcup _{{m,n\geq 0}}\bigsqcup _{{y\in {\text{Crit}}(L_{n},L_{{m+n}})}}\overline {\mathcal {M}}^{0}(y;\underline {x}';\nu )\times \overline {\mathcal {M}}^{0}(x_{0};\underline {x},y,\underline {x}'';\nu ).




Finally, we need to check that for each pair (b,b')\in \overline {\mathcal {M}}^{0}(x_{0};\underline {x},y,\underline {x}'';\nu )\times \overline {\mathcal {M}}^{0}(y;\underline {x}';\nu ), when considered as boundary point (b,b')\in \partial \overline {\mathcal {M}}^{1}(x_{0};x_{1},\ldots ,x_{d};\nu ), has symplectic area \omega ((b,b'))=\omega (b)+\omega (b') and weight function {\text{w}}((b,b'))=(-1)^{{\|\underline x\|}}{\text{w}}(b){\text{w}}(b').


[Expand]

Analysis TODO:

Retrieved from "http://www.polyfolds.org/index.php?title=Regularized_moduli_spaces&oldid=452"